@TingAstro

Yuan-Sen Ting

The Ohio State University

Transcending the Limits of Astrostatistics
 with Deep Learning

Large-scale structure

Cosmology

Euclid, DESI, PFS, ROMAN, CSST

Most phenomenology in physics is a complex stochastic field

Credit: Illustris

Large-scale structure

Cosmology

Credit: Illustris

Most phenomenology in physics is a complex stochastic field

Cosmic Reionisation

SKA, HERA, MWA

Most phenomenology in physics is a complex stochastic field

Cosmology

Credit: ESO

GAIA Satellite

Galactic physics

Motions of a billion stars

SDSS-V, 4MOST, MUST

Most phenomenology in physics is a complex stochastic field

Credit: ESA

Posterior

Prior

Likelihood

P ( physics | observation )      p ( observation | physics ) * p ( physics )

\propto

Oh well, statistics

P ( price | car )         p ( car | price ) * p ( price )

\propto

Prior

P ( price | car ) = p ( car | price ) * p ( price )

Likelihood

\propto

P ( price | car ) = p ( car | price ) * p ( price )

Posterior

\propto
\propto

P ( physics | observation )      p ( observation | physics ) * p ( physics )

Very high dimensional

Bayesian statistics has been limited to a few domains in astro.

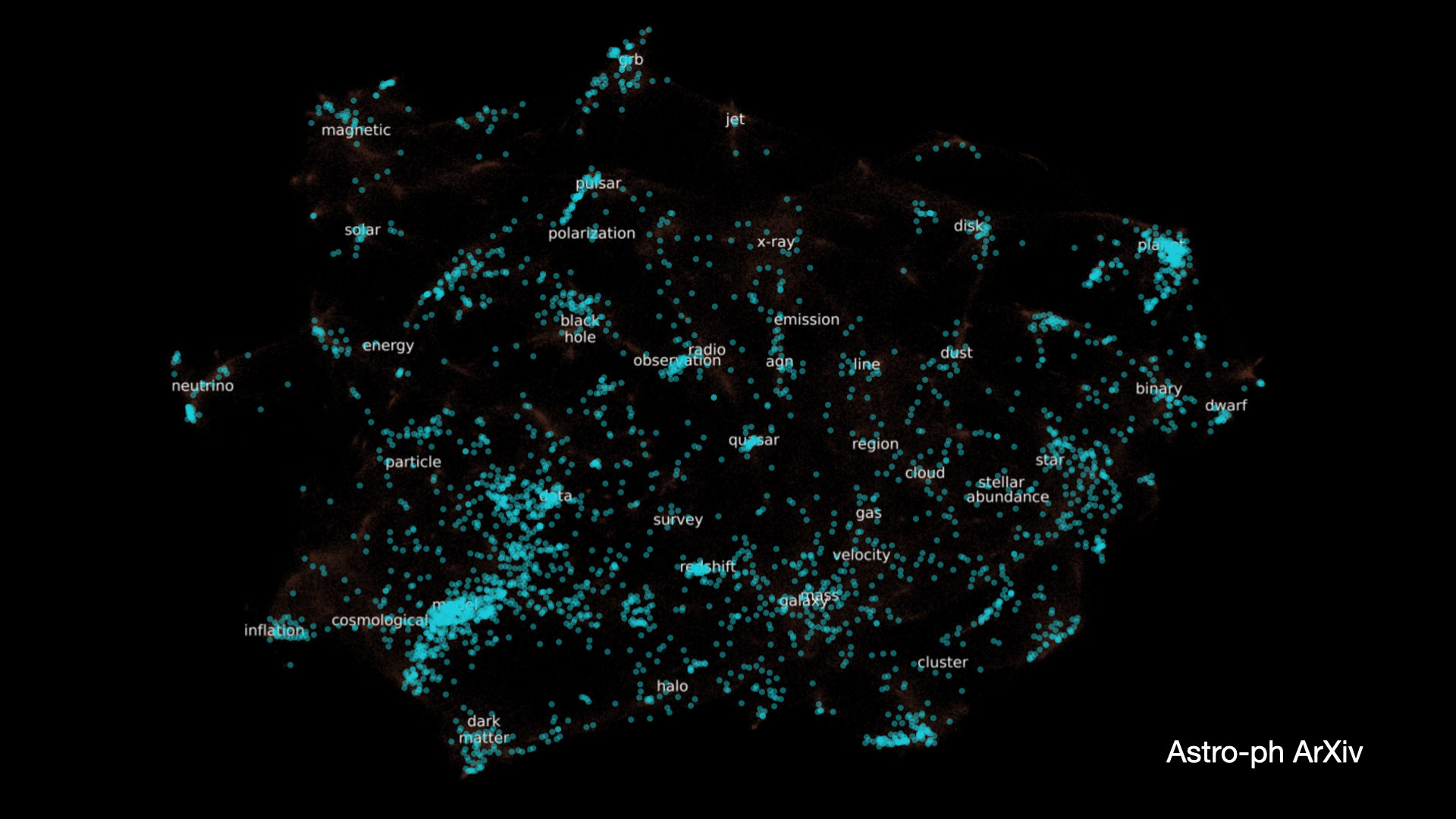
Credit : arxivsorter.org

Astro-ph arXiv

Credit : arxivsorter.org

Nobel Prize 11, 19

Exoplanet

Pulsar

Nobel Prize 74, 93

Nobel Prize 19

Bayesian statistics has been limited to a few domains in astro.

Astro-ph arXiv

Cosmology

Credit : arxivsorter.org

Exoplanet

Plasma
Turbulence

Nobel Prize 11, 19

Nobel Prize 19

Pulsar

Nobel Prize 74, 93

Cosmology

Star Formation,
Galaxy Evolution,
Black Hole Physics

Astrostatistics

Gaussian / "Linear"

Deep Learning

Non-Gaussian /
"Non-Linear"

(e.g. early cosmology)

(e.g. reionisation, turbulence, galaxy evolution, star formation)

Mathematics of information - better summary statistics

Generative AI - Simulation-Based Inferences

How to quantify a high-dimensional likelihood 

"One of the principal objects of research in my department of knowledge is to find the point of view from which the subject appears in the greatest simplicity"

- Gibbs

Complexity

Stochasticity

My niece 

E.g.,

orientation

projecting out uninformative variability

"Physical Modelling"

I(R|b,n,R_e) \sim \exp\bigg(-b\Big[\big(\frac{R}{R_e}\big)^{1/n} -1\Big]\bigg)

Sersic profile

(or "structures")

("uninformative" variances)

Complexity

Stochasticity

Cosmic Microwave Background

Reionization

Intergalactic Medium Tomography

Large-Scale Structure

(or "structures")

("uninformative" variances)

Characterising stochastic fields is challenging

Gaussian

Non-Gaussian

Simple

Complex

Power spectrum

Power spectrum

Complexity

Stochasticity

(or "structures")

("uninformative" variances)

These two images have the same power spectrum

Gaining mathematical insights from deep learning

(1) Convolution

(2) Non-linearity

(or "activation function")

e.g., ReLU

(4) Iterate

e.g., tanh, sigmoid

(3) Averaging

I(\vec{x})

Why convolutional neural networks work ?

Alchemy ???

Not really ...

These two images have the same power spectrum

p(x)
x

Consider a single random variable

x \sim p(x)

From why power spectrum fails to how CNNs work : a 1D case

p(x)
x

Consider a single random variable

x \sim p(x)

From why power spectrum fails to how CNNs work : a 1D case

p(x)
x

Consider a single random variable

x \sim p(x)

In 1D, power spectrum is equivalent to taking the second moment

\langle x^2 \rangle_{x \sim p(x)}

Variance

Skewness

The "tail" differentiates these two patterns

From why power spectrum fails to how CNNs work : a 1D case

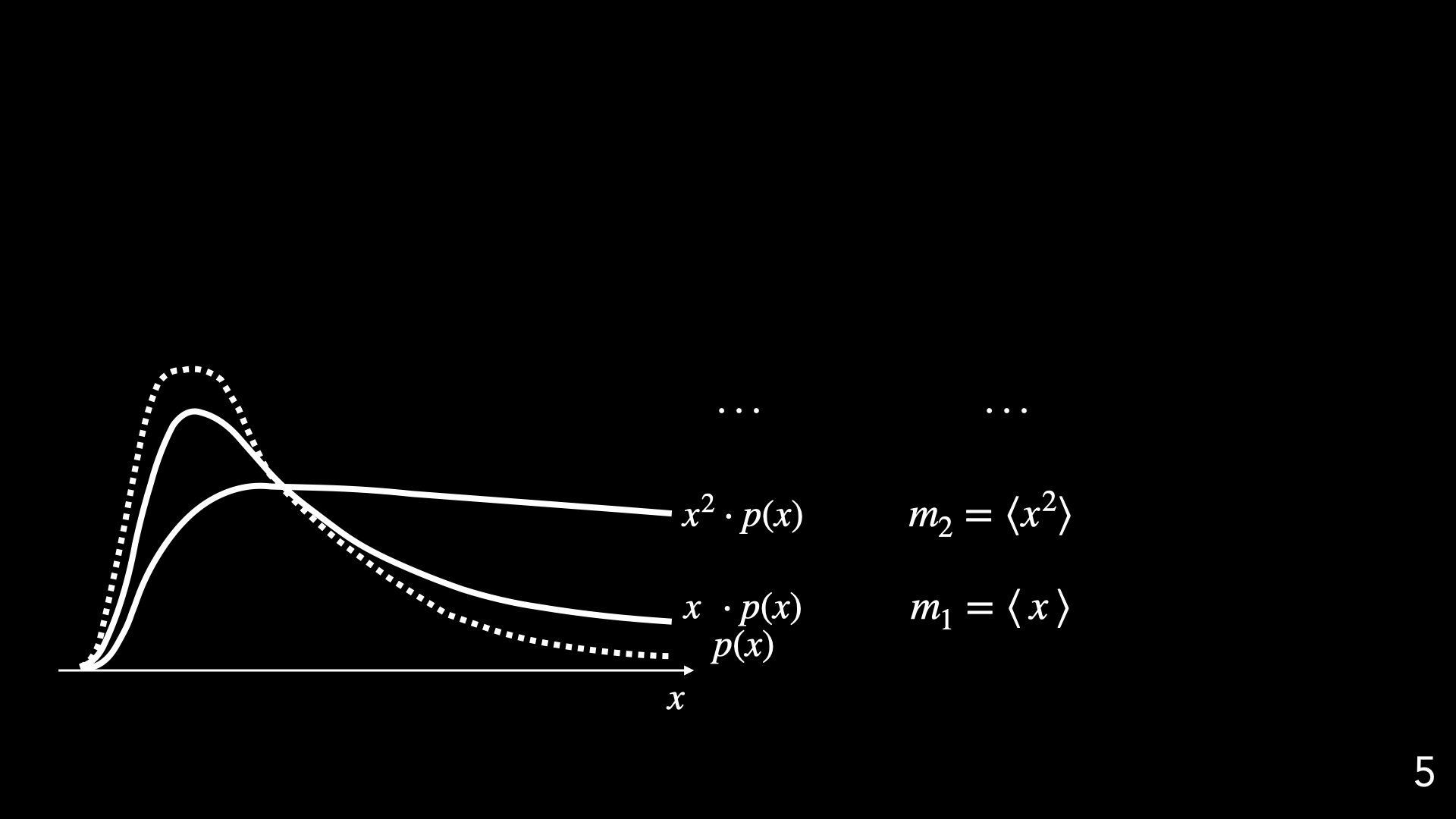
Quantifying distribution functions with higher-order moments?

p(x)
x

Consider a single random variable

x \sim p(x)

Variance

Skewness

Skewness defines locality

Classical lores : characterizing

p(x)

with all its moments

\langle x \rangle, \langle x^2 \rangle, \cdots, \langle x^n \rangle
p(x)
x

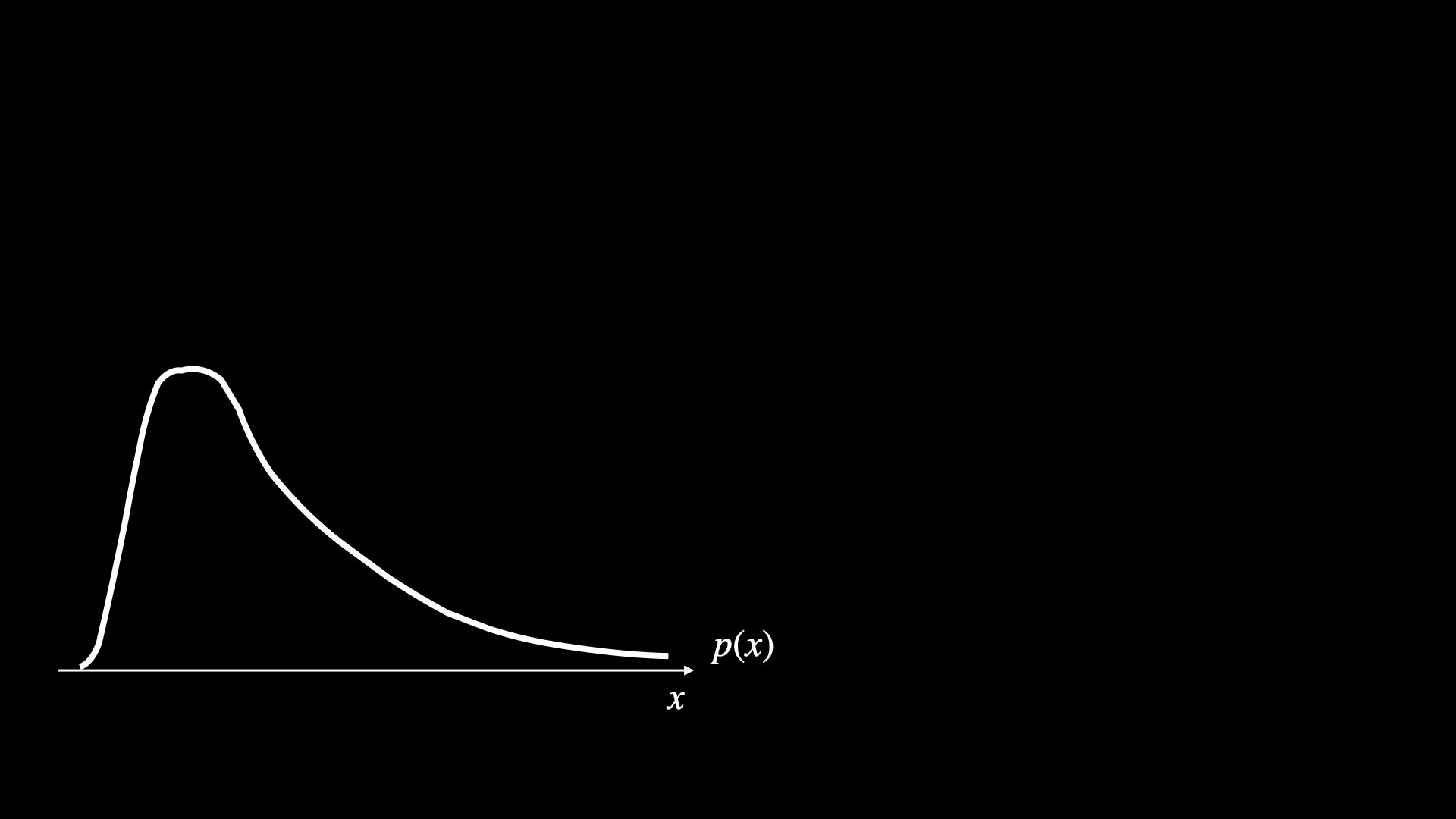
Heavy tail
(Non-Gaussian)

Naively taking higher-order moments is not a good idea

p(x)
x
x \cdot p(x)
x^2 \cdot p(x)
\langle x \rangle
\langle x^2 \rangle

Naively taking higher-order moments is not a good idea

p(x)
x
x \cdot p(x)
x^2 \cdot p(x)
\langle x \rangle
\langle x^2 \rangle
p(x)
x
x \cdot p(x)
x^2 \cdot p(x)
\langle x \rangle
\langle x^2 \rangle
x^n \cdot p(x)
\langle x^n \rangle

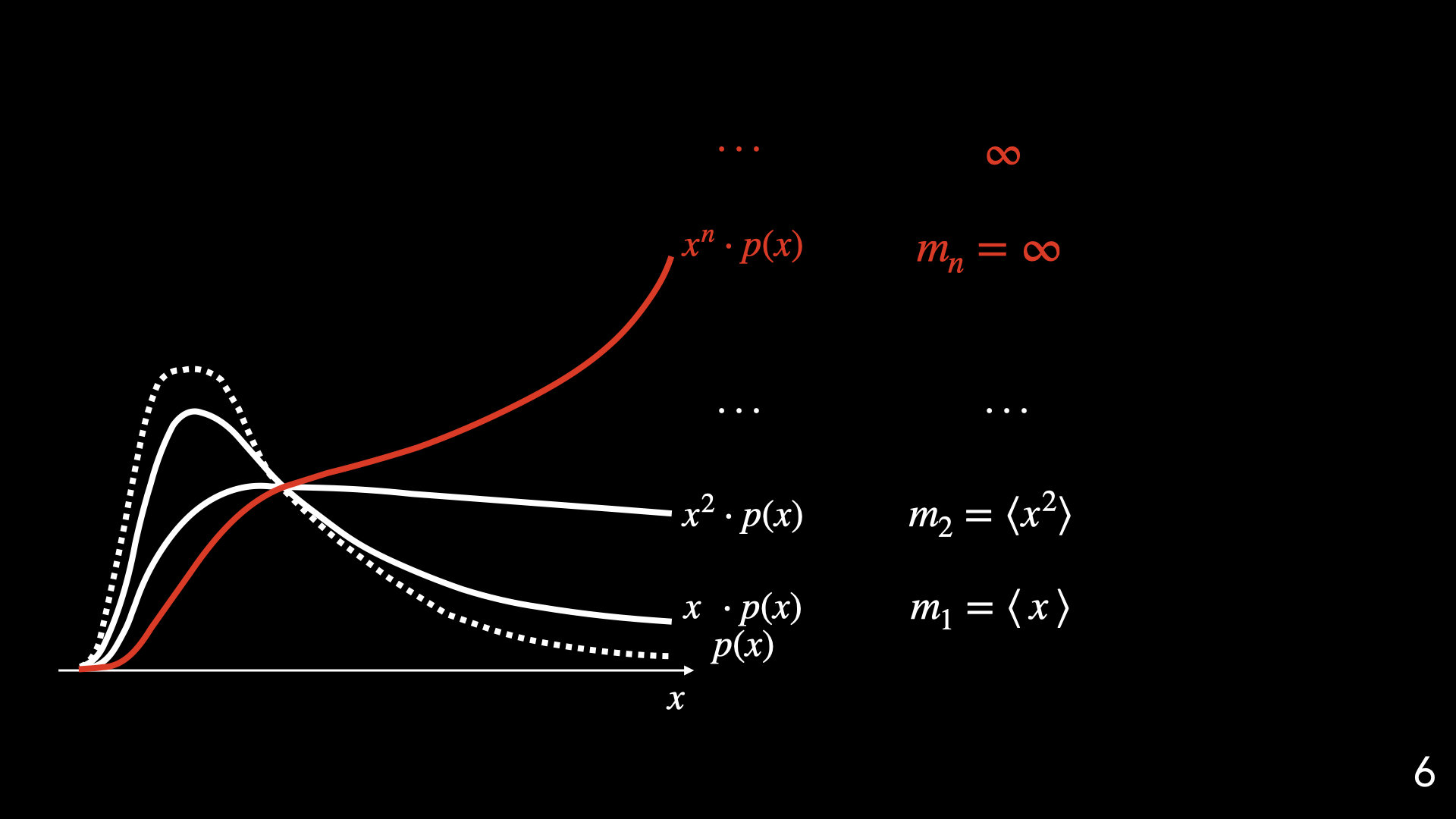
Depend critically on the "outliers"; subjected to the sampling noise

The estimates are noisy

Naively taking higher-order moments is not a good idea

How to characterize "higher moments" via low-order operations

p(x)
x
s_0 = \langle x \rangle
s_0
x_1 = \big| \, x - \langle x \rangle \, \big|

"Folding"

p(x)

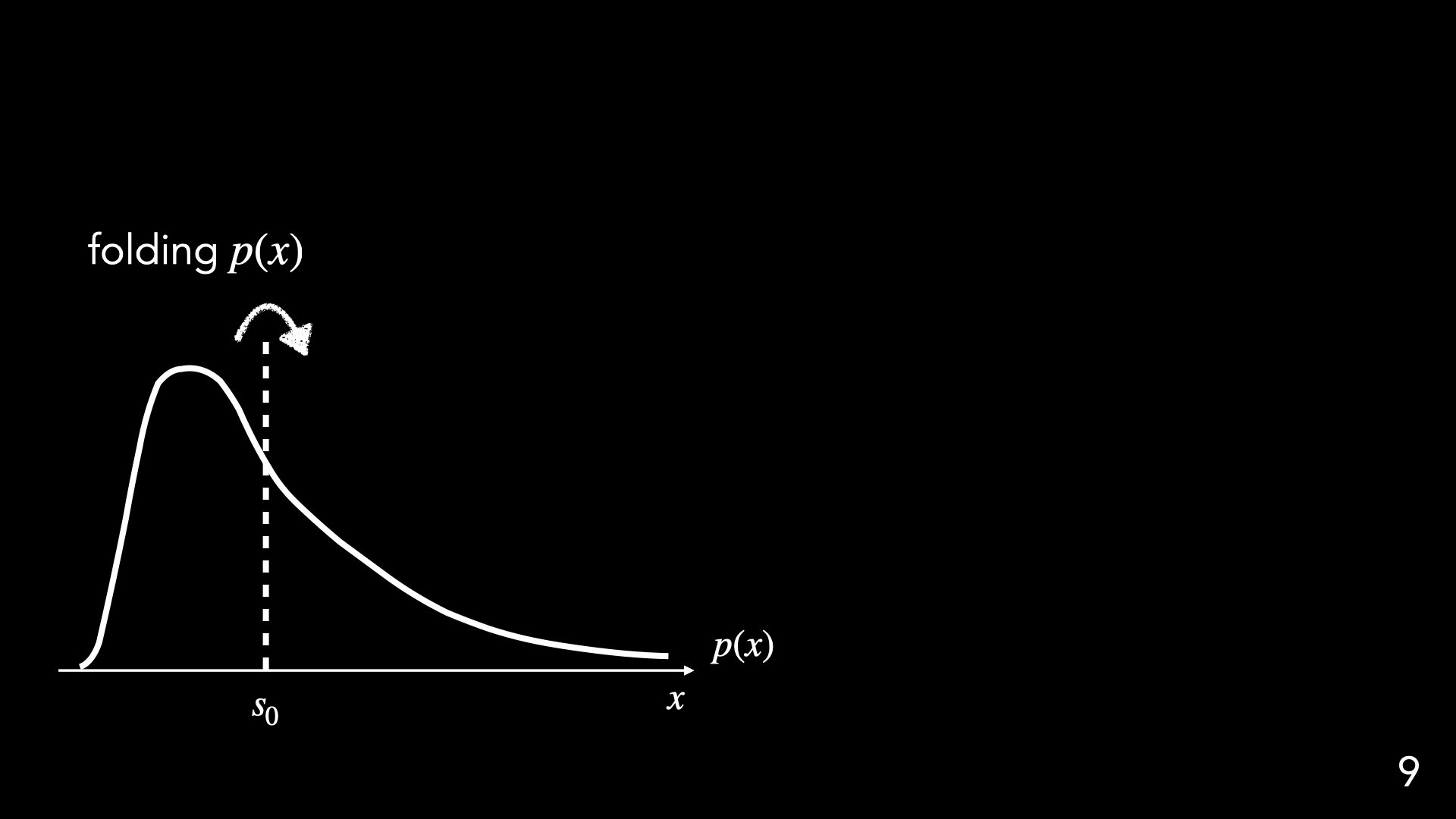
"Folding" = non-linear operation + averaging

p(x)
x
s_0

"Folding"

p(x)
s_1
s_1 = \langle x_1 \rangle,
s_0 = \langle x \rangle
x_1 = \big| \, x - \langle x \rangle \, \big|

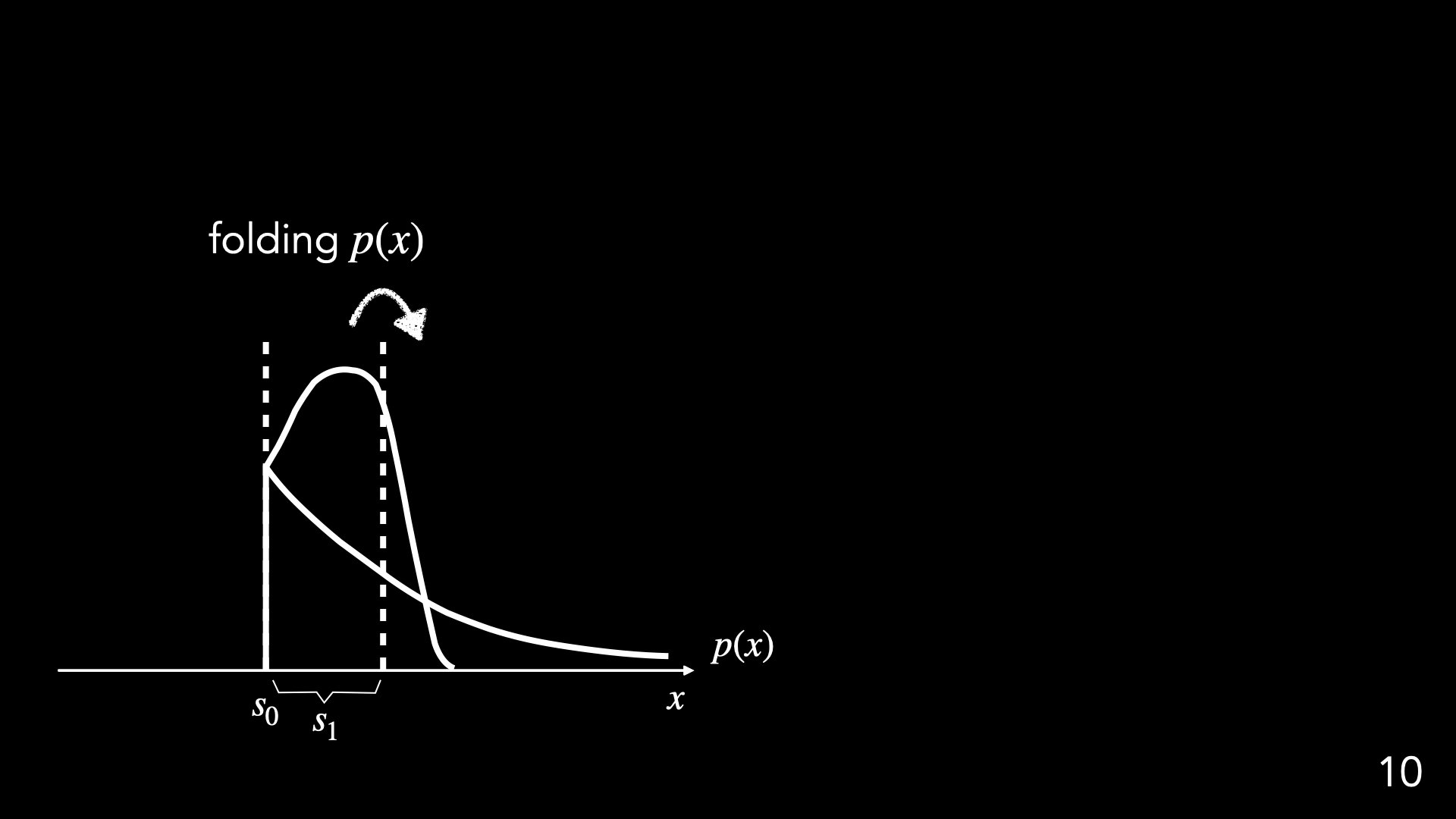
"Folding" = non-linear operation + averaging

How to characterize "higher moments" via low-order operations

p(x)
x
s_0
s_1

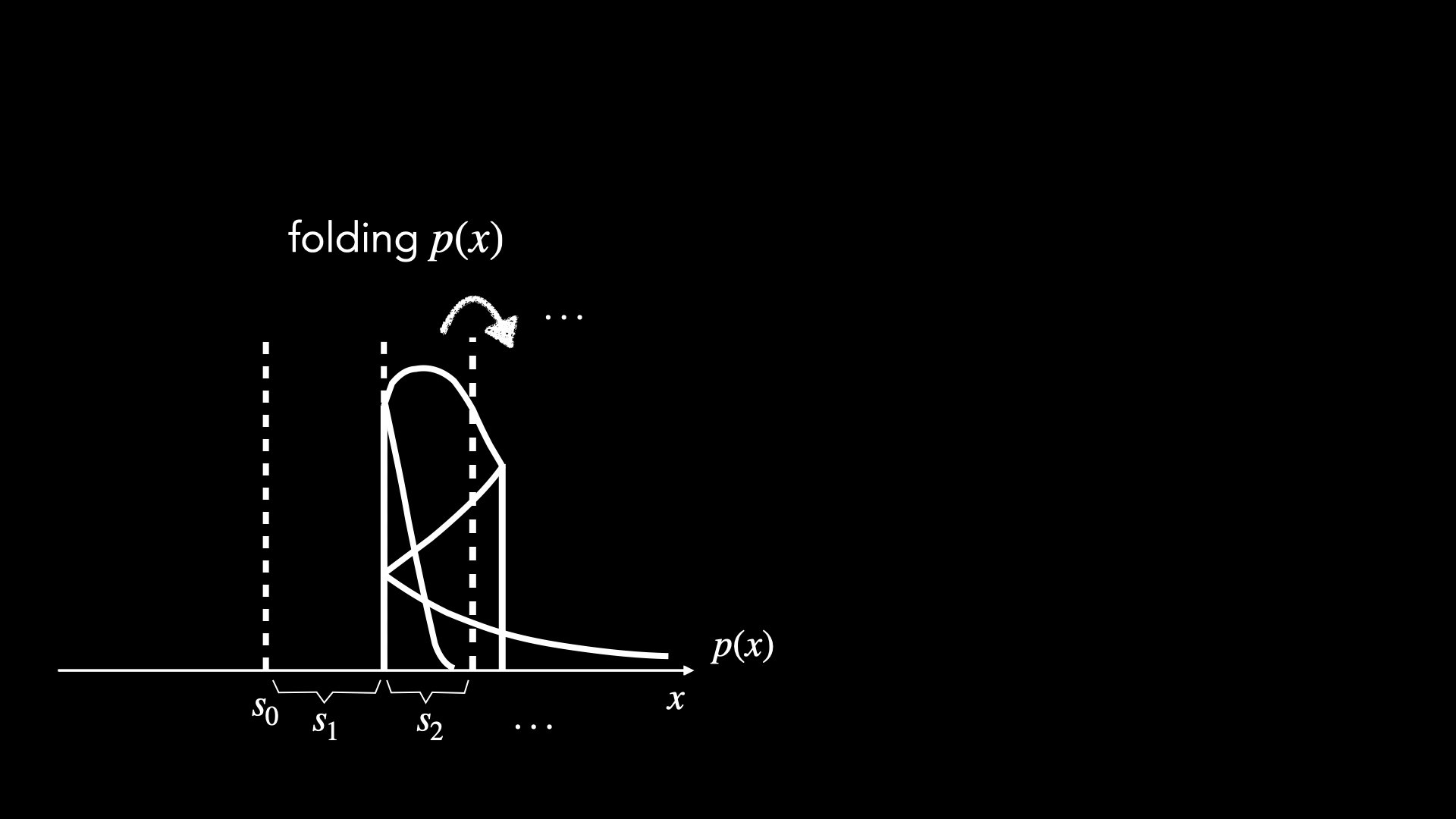
"Folding"

p(x)
s_2
s_1 = \langle x_1 \rangle,
s_0 = \langle x \rangle
x_1 = \big| \, x - \langle x \rangle \, \big|
x_2 = \big| \, x_1 - \langle x_1 \rangle \, \big|
s_2 = \langle x_2 \rangle,

Linear order with respect to

x

stable and robust summary statistcs

How to characterize "higher moments" via low-order operations

(or "activation function")

e.g., ReLU

e.g., tanh, sigmoid

I(\vec{x})

A necessary set of operations to capture high-order moments robustly

Toward an understanding of the operations in CNNs

(1) Convolution

(2) Non-linearity

(4) Iterate

(3) Averaging

Scattering transform: a better analytic tool inspired by CNNs

Case Study : Weak Lensing

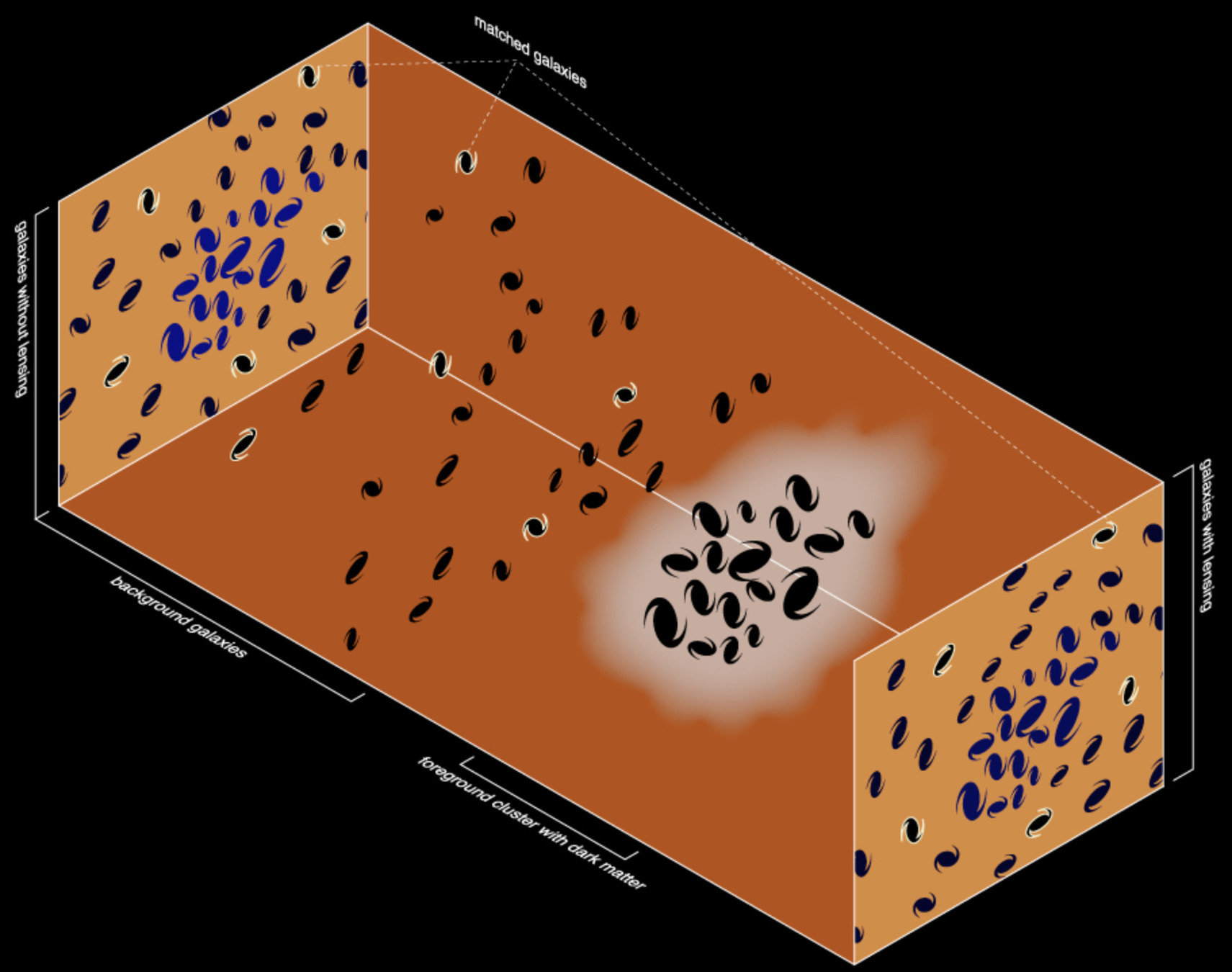
Credit: Wikipedia

Background galaxies

Foreground dark matter

Unlensed

Lensed

Vary cosmological parameters

(\Omega_M, \sigma_8)

0.9

0.8

0.7

0.25

0.30

0.35

0.40

\Omega_M
\sigma_8

Classical summary statistics only give weak constraints

Dark Matter Density

Growth Amplitude

Power spectrum fails to distinguish the intricate differences between the two maps

Power spectrum

0.9

0.8

0.7

0.25

0.30

0.35

0.40

\Omega_M
\sigma_8

Power spectrum

Dark Matter Density

Growth Amplitude

Cheng, YST, Menard & Bruna + 20

Scattering

Scattering transform gives better constraints in weak lensing

Transform

International Astrostatistics Association Award

Vary cosmological parameters

(\Omega_M, \sigma_8)

0.9

0.8

0.7

0.25

0.30

0.35

0.40

\Omega_M
\sigma_8

Classical feature extraction only give weak constraints

Dark Matter Density

Growth Amplitude

Power spectrum fails to distinguish the intricate differences between the two maps

Power spectrum

On detecting parity violation beyond 4-point correlation function

On detecting parity violation beyond 4-point correlation function

On detecting parity violation beyond 4-point correlation function

vs.

Parity violating

Non violating

Scattering transform leads to much stronger PV detection

Craigie, Taylor, YST+ 24; Taylor, Craigie, YST+ 24

0

20

40

60

80

50

200

800

120

# Training patches of the sky

Detection Significance 

Scattering Tranform

Convolutional Neural Network

Mathematics of information - better summary statistics

Generative AI - Simulation-Based Inferences

How to quantify a high-dimensional likelihood 

Oh well, statistics

\propto

P ( physics | observation )      p ( observation | physics ) * p ( physics )

Describing the high-dimensional likelihood as it is

Simulation-Based Inference
with deep generative models

Prompt :

Kangaroo operating telescope,
looking into space

Deep generative models: generations with prompts

OpenAI's Dall-E 2

Text Prompt

Images 

Generative models : a high-D density estimation problem

All possible images

Kangaroo operating telescope,
looking into space

p~(~~~~~~~~~~~|~~~~~~~~~~~~~~~~~~~)

Kangaroo operating telescope

p~(~~~~~~~~~~~|~~~~~~~~~~~~~~~~~~~)

Cosmological parameters

p~(~~~~~~~~~~~|~~~~~~~~~~~~~~~~~)
p~(~~~~~~~~~~~~~~~~~|~~~~~~~~~~~)~ = ~

Likelihood

Posterior

p~(~~~~~~~~~~~~~~~~)

Prior

Simulation-based Inferences (SBI) / Likelihood-free Inferences

Cosmological parameters

Cosmological parameters

Cosmological parameters

Images 

p~(~~~~~~~~~~~~~~~~~|~~~~~~~~~~~)

Cosmological parameters

Text Prompt

Cosmological parameters

Learning all cosmic realizations from simulations with SBI

Deep generative models have come a long way

More dated models (e.g., GAN) are not suitable for AI x Astro

Zakharov+ 19

Generator
( machine 1)

Discriminator
( machine 2 )

Generator

Discriminator

Lack of diversity

GAN generates plausible results but suffer from mode collapse

Modern deep learning is much more resilient to mode collapse

Neural Network

Maximum Likelihood Estimation

f: x \mapsto z

Normalizing Flows
Diffusion Models

e.g., YST & Weinberg 21, Tang & YST 22

Assessing quantitatively the quality of generative models

Zhao, YST+ 2023

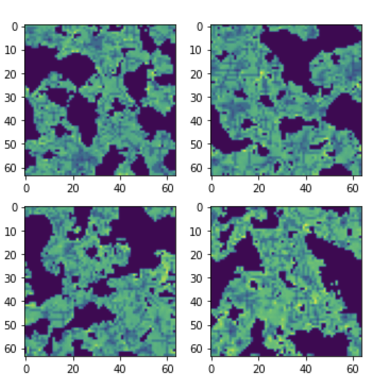
Truth (simulations) 

Frechet distance:

~0.2 (truth x truth)

GAN (StyleGAN 2)

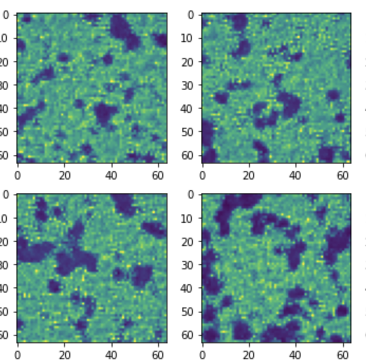
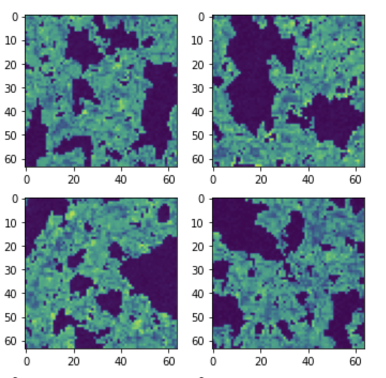
Diffusion Models (DM)

~2-2.5 (truth x GAN)

~0.4 (truth x DM) 

0.9

0.8

0.7

0.2

0.3

0.4

0.5

\Omega_M
\sigma_8

Power spectrum

Dark Matter Density

Growth Amplitude

Dai & Seljak, 2022

Normalizing Flow

Constraining weak lensing cosmological parameters with SBI

The idea of simulation-based inferences goes beyond just the study of cosmology

Present day galaxies - results of galaxy merger events

A shameless promotion of 1990s Japanese anime

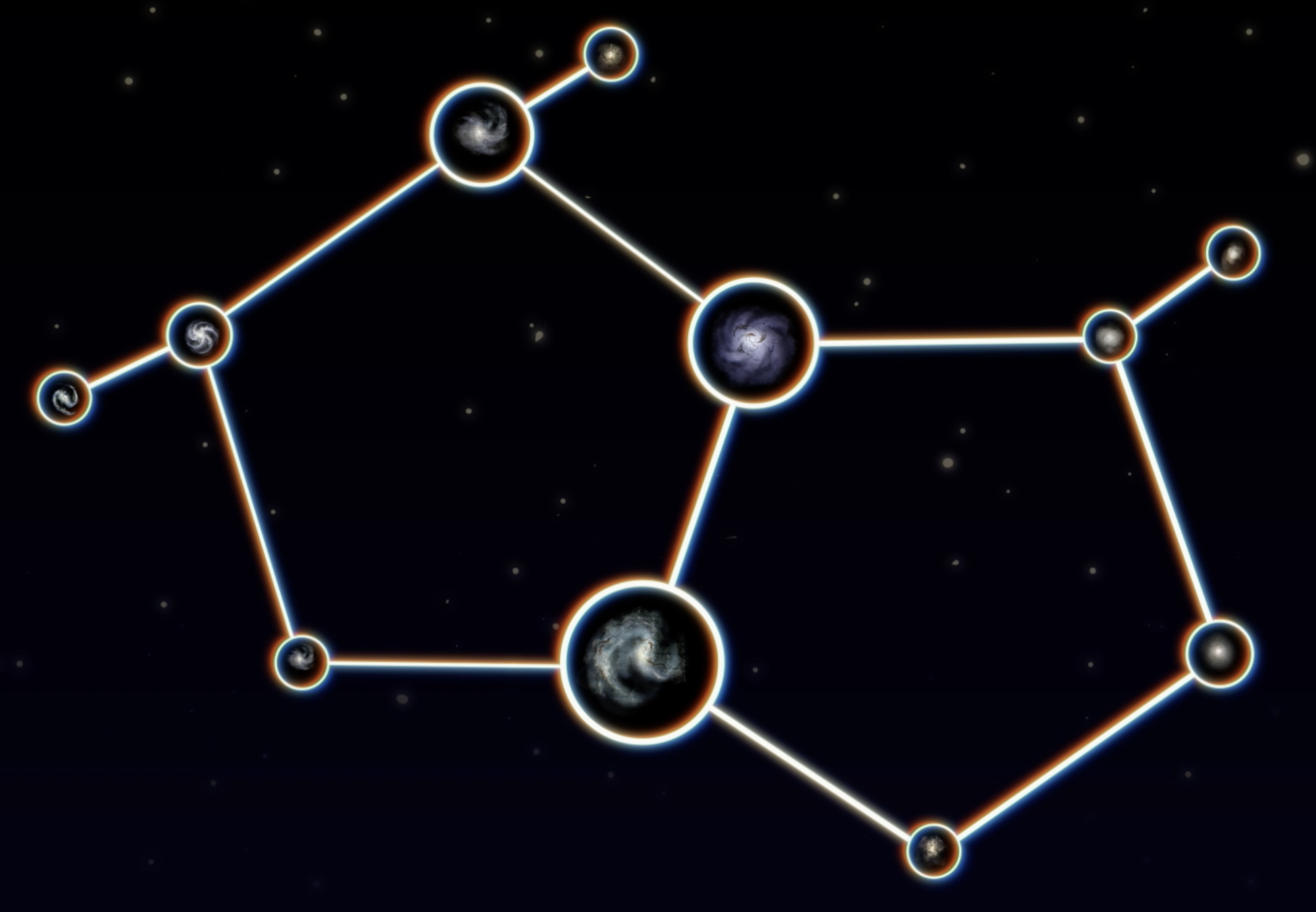
Image = fixed dimension

Dealing with graphs is challenging - varying dimensionality

Graph = varying dimension

Dealing with graphs is challenging - huge redundancy

Graph deep generative models have drastically improved

Blackhole mass

Blackhole accretion

Gas metallicity

Stellar metallicity

Stellar mass

Rotational curve vmax

Velocity dispersion

Stellar mass

For individual nodes :

Merging redshift

Pairwise distances

Tang & YST, 2022, ICML W Spotlight

p~(~~~~~~~~~~~~~~~~~~~|~~~~~~~~~~~)

present day

10 billion years ago

Distilling knowledge from cosmological simulations

p~(~~~~~~~~~~~~~~~~~|~~~~~~~~~~~)
p~(~~~~~~~~~~~|~~~~~~~~~~~~~~~~~)~ = ~

Likelihood

Posterior

p~(~~~~~~~~~~~)

Prior

Simulation-Based Inferences with galaxy progenitor systems

p~(~~~~~~~~~~~|~~~~~~~~~~~~~~~~~)

Simulation-Based Inferences with galaxy progenitor systems

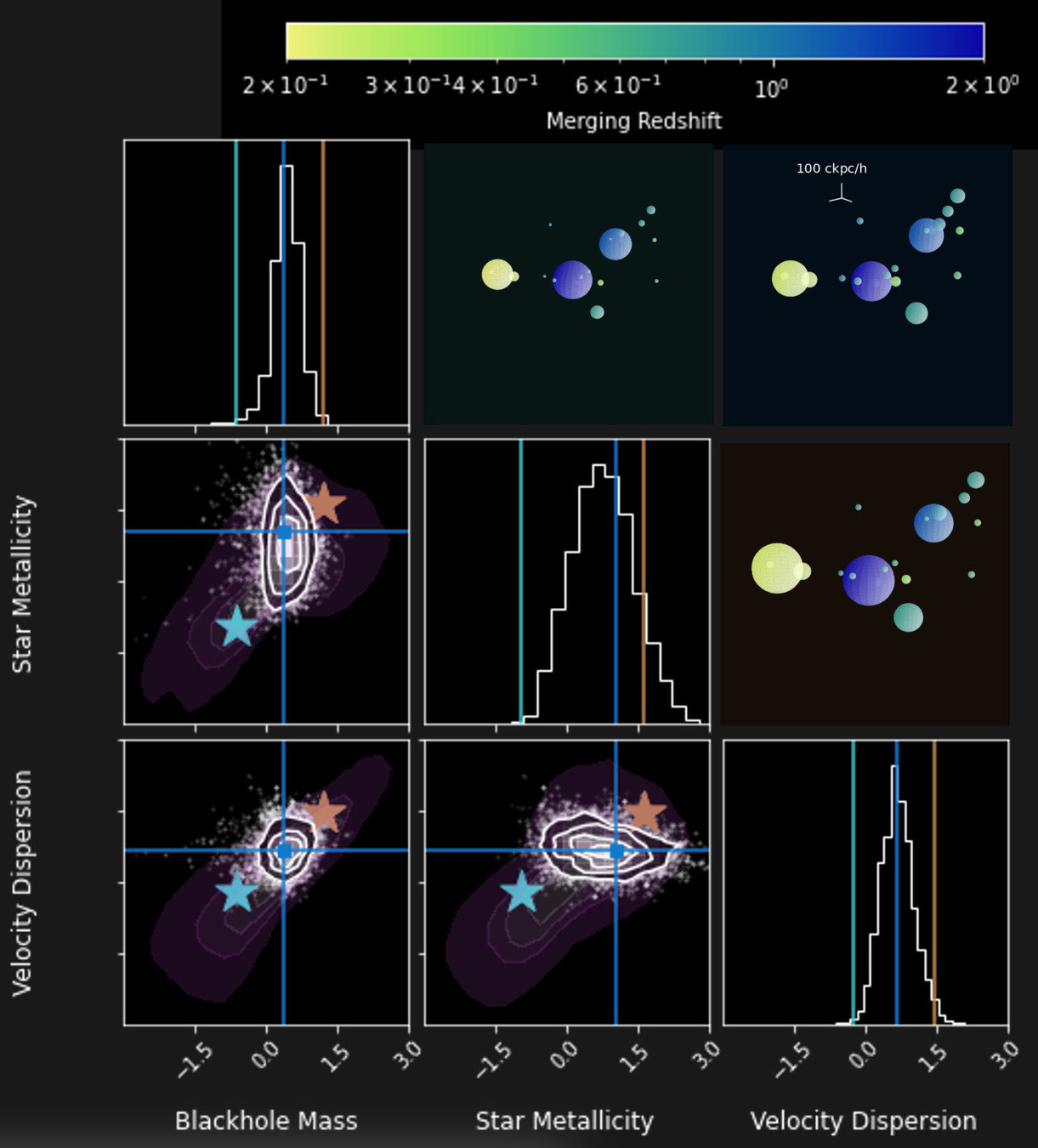
Stellar
Metallicity

Velocity
Dispersion

Blackhole
Mass

Stellar
Metallicity

Velocity
Dispersion

0.2

0.3

0.4

0.6

1.0

2.0

Merging Redshift

Tang & YST, 2022

p~(~~~~~~~~~~~~~~~~~~~|~~~~~~~~~~~)

Normal

Outlier

Likelihood =

Out-of-distribution ( outliers ) detections

Normal

Outlier

Log likelihood

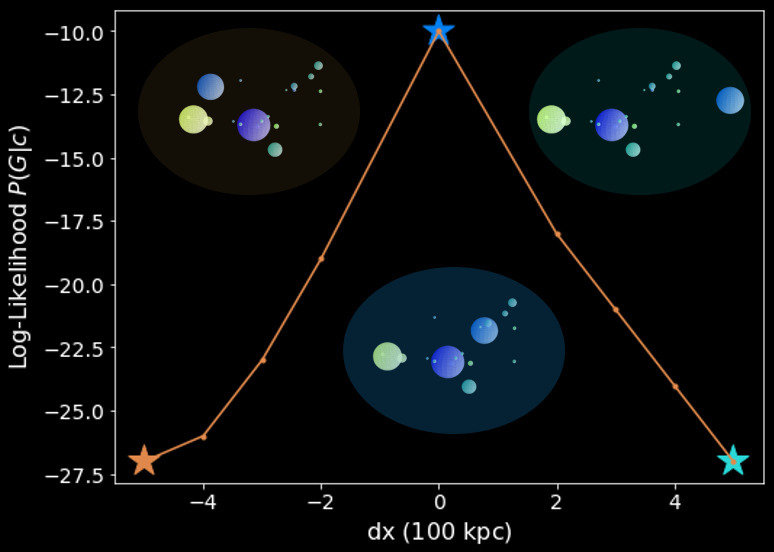
Displacement [ 100 kpc ]

p~(~~~~~~~~~~~~~~)

Simulated system

0.2

0.3

0.4

0.6

1.0

2.0

Merging Redshift

Tang & Ting, 2022

Out-of-distribution ( outliers ) detections

Normal

Outlier

Log likelihood

p~(~~~~~~~~~~~~~~)

Out-of-distribution ( outliers ) detections

Displacement [ 100 kpc ]

Tang & Ting, 2022

Summary :

Modern-day large surveys have revealed ever more complex patterns and structures

Classical astrostatistics tools struggle to deal with high-dimensional non-Gaussian observations

Summary :

Mathematics of information from ML has led to powerful analytic tools (e.g., scattering transform) to characterize complex systems

The success of deep generative models provides new possibilities to directly compare simulations with observations

Modern-day large surveys have revealed ever more complex patterns and structures

Classical astrostatistics tools struggle to deal with high-dimensional non-Gaussian observations

Extra Slides

Cosmic Reionisation

Cosmology

Imaging the cosmic dawn/reionisation with SKA

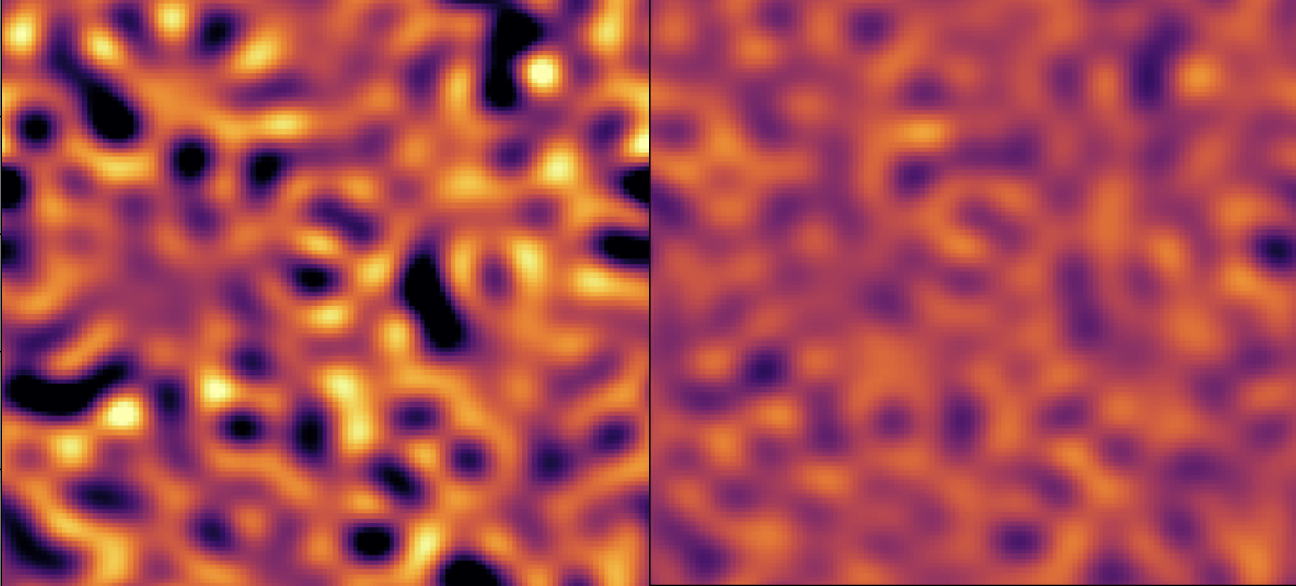
Length [ Mpc ]

0

50

100

150

200

250

0

50

100

150

200

250

0

50

100

150

200

250

Scattering transform yields 3x stronger constraints for SKA

Power spectrum

Scattering transform

0.0

Fraction of gas in galaxies, and

Ionization photon escape fraction, and

Greig, YST & Kaurov, 22, 23

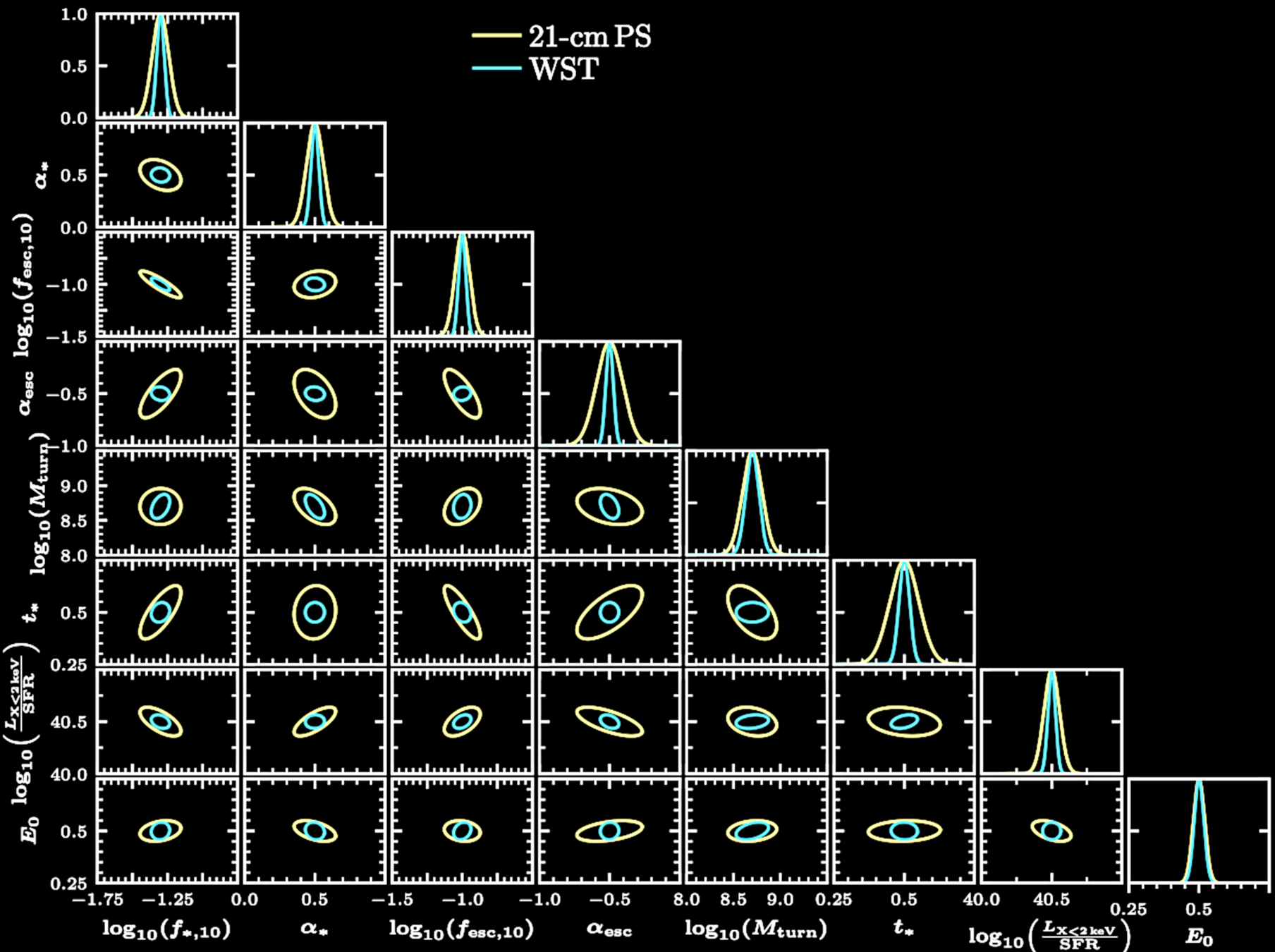
its dependence on the halo mass

its dependence on the halo mass

Galaxy mass below which star formation is suppressed

Star formation evolution time scale

Emisitivity in X-ray

X-ray escape threshold

However observation is of high dimensional ...

Asteroseismology

P ( physics | observation )      p ( observation | physics ) * p ( physics )

Very high dimensional

\propto

The bottleneck of astrostatistics ...

Observation

Physics

Summary Statistics

10^4-10^6 D
10-100 \,D

Characterizaton

Theory

\propto

The bottleneck of astrostatistics ...

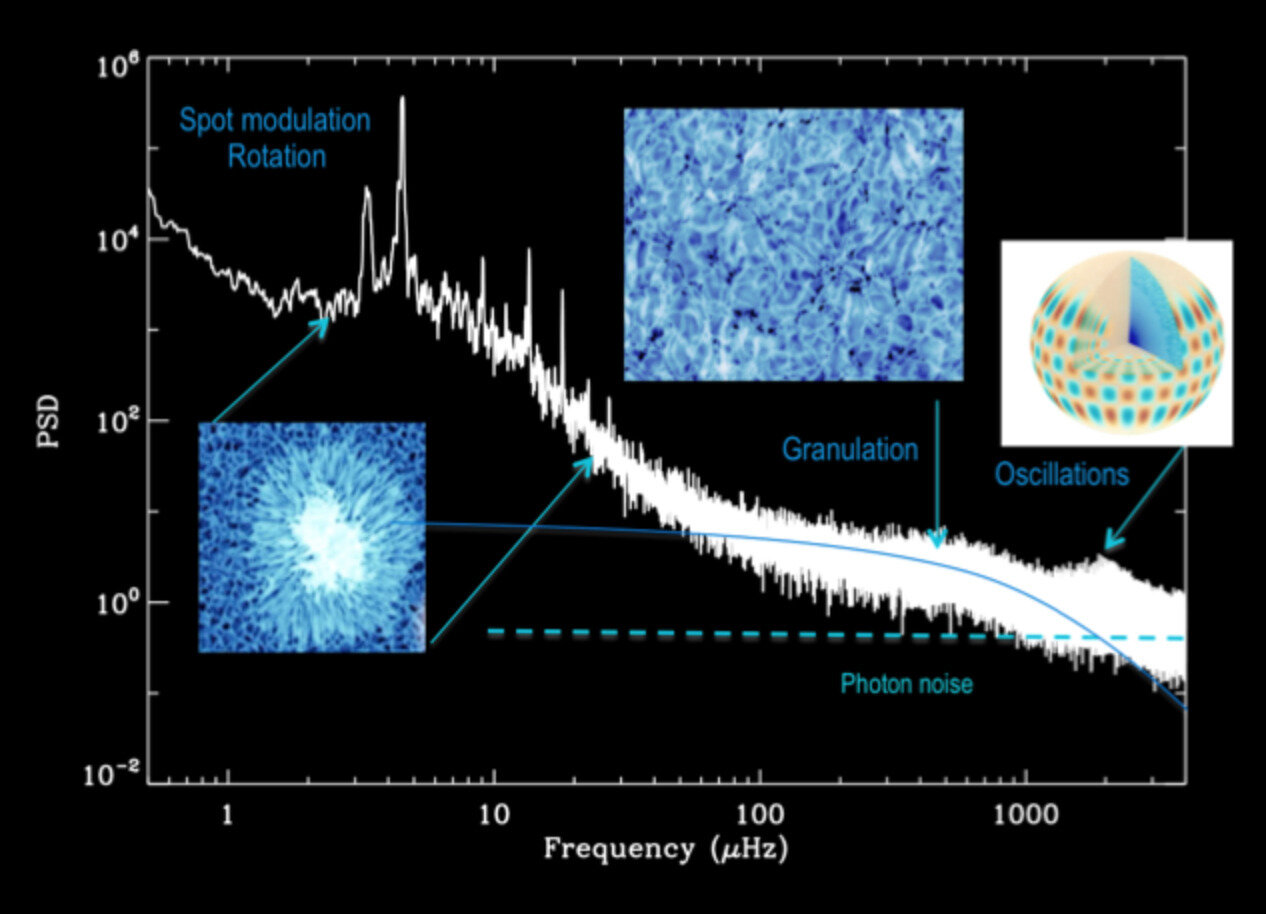
Frequency

Power Spectral Density

\nu_{\rm max}
p(\nu_{\rm max} | {\rm physics} )

Oscillation

Granulation

P ( physics | observation )      p ( observation | physics ) * p ( physics )

Observation

Physics

Summary Statistics

10^4-10^6 D
10-100 \,D

Theory

Imperfect physics
= Information Loss

Characterizaton

Why the hype with deep learning ?

Curse of Dimensionality

Deep Learning

Curse of dimensionality: a exponentially large data set is needed

DL can describe high-dimensinoal space with a finite data

Underlining the success of deep learning are symmetries

Symmetries make deep learning more sample efficient

"I suppose it is tempting, if the only tool you have is a hammer, to treat everything as if it were a nail"

Abraham Maslow

Power Spectrum

Convolutional Neural Networks

Scattering Transform

15 coefficients

37 coefficients

10

100

1000

noiseless

DES

(\Omega_M,\sigma_8)

figure of merit

Galaxy number density

performance is on par with

Scattering transform's

CNNs

Better

Euclid / CSST / Roman

Rubin

Complexity

Stochasticity

Human heuristics
( power spectrum )

(or "structures")

("uninformative" variances)

Scattering Transform

Gaussian

Non-Gaussian

Simple

Complex

 Credit: Shangjia Zhang, Zhaohuan Zhu

Characterizing the protoplanetary disk observations

Yuan, YST+ in prep.

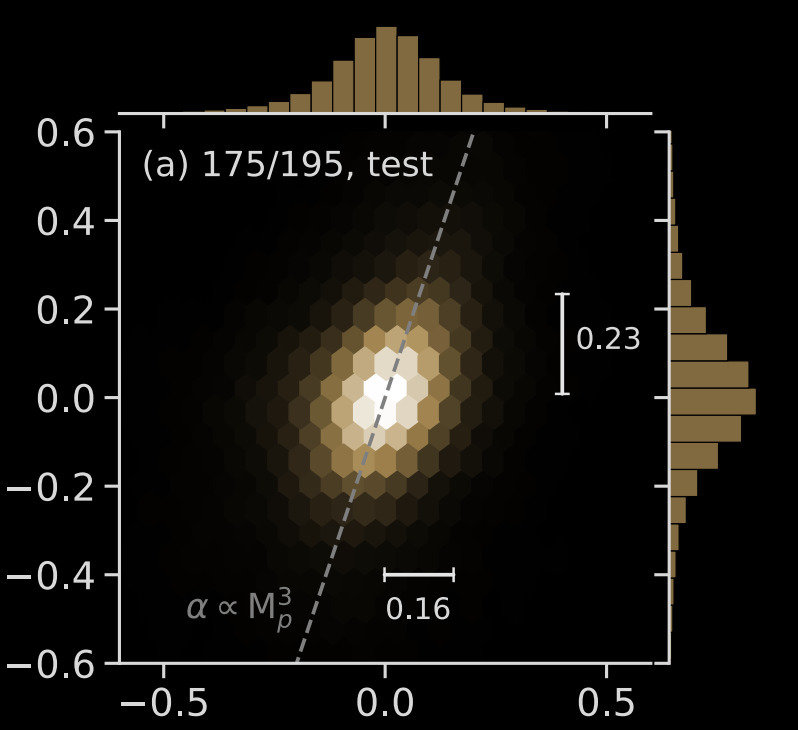
Log Planet Mass [ inferred - truth ]

Log Viscosity [ inferred - truth ]

Zhang+22

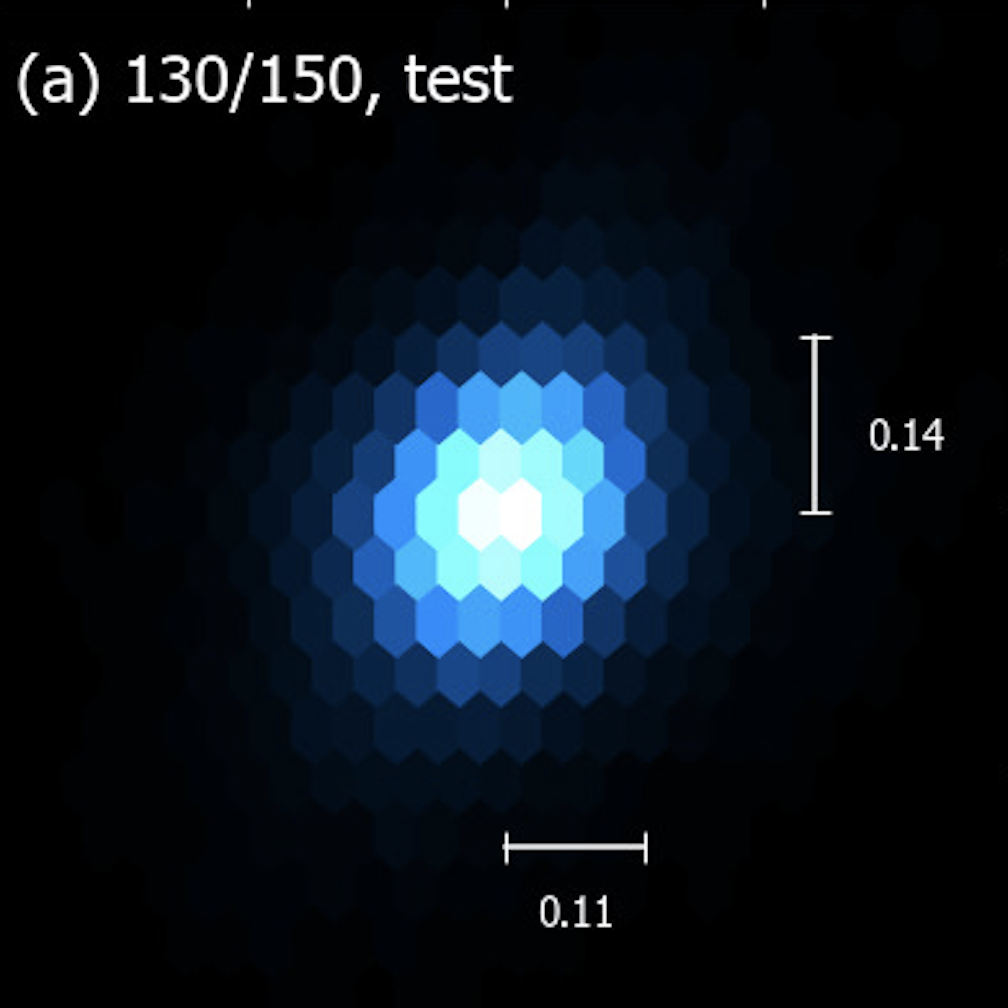
This study
( Scattering Transform)

0.11

0.14

Characterizing the protoplanetary disk observations

Mock data

A theoretical understanding of deep learning
makes a big difference

Neural Networks

Observation

The ML tool with the relevant symmetries

Blindly applying machine learning 

Classical tool
(e.g., power spectrum)

stellar interior,
surface gravity

Convolutional
Neural Network ???

(e.g., Hon+17,18, Blancanto+22)

CNNs do not have the right "inductive bias" for time series

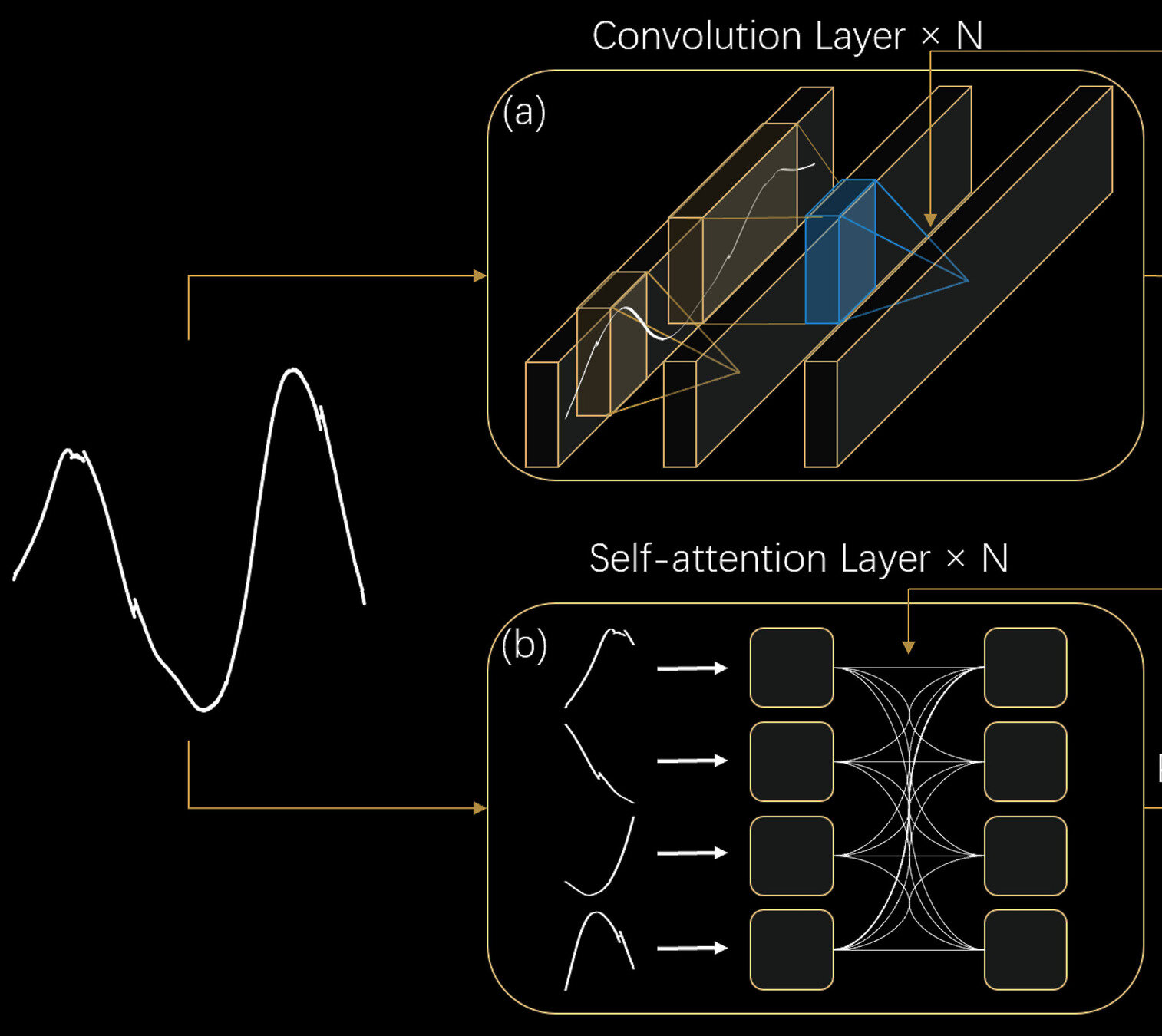
Convolutional Neural Networks

Local perceptive field

Transformer

Long-range information

The cat sat on the mat and licked its paws

在这深宫之中，你我皆是棋子，有时你在用我，有时我在用你，唯有互相利用，方能在这混乱的权力游戏中求得一线生机。

The foundation of Large Language Models: Attention

The foundation of Large Language Models: Attention

Extracting long-range information from stellar light curves

Pan, YST & Yu 22, 24

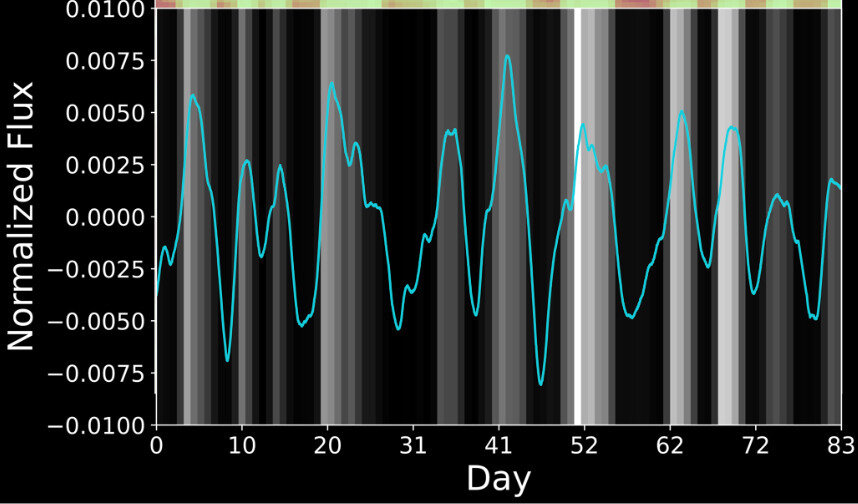
Kepler's Light Curve

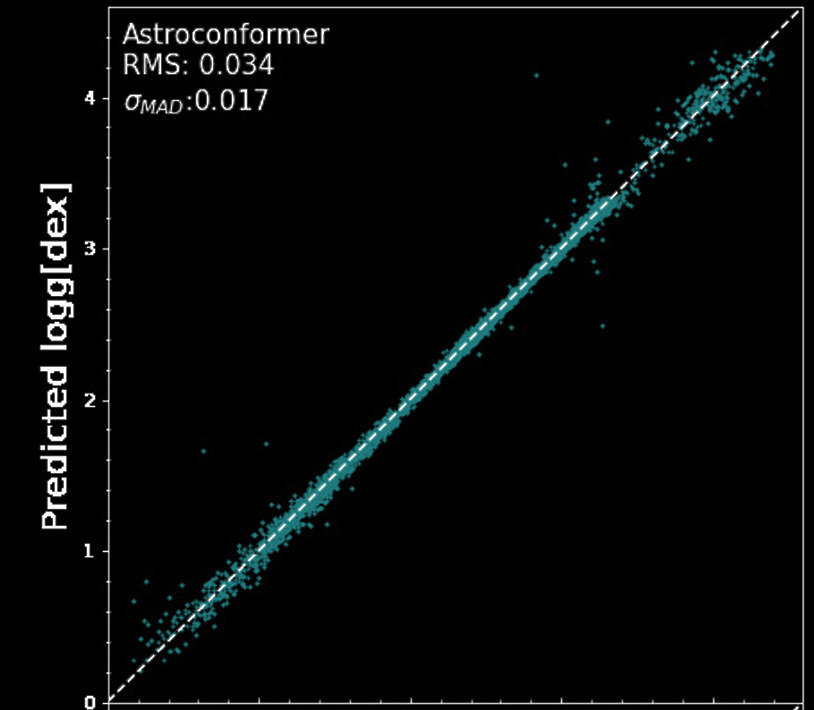
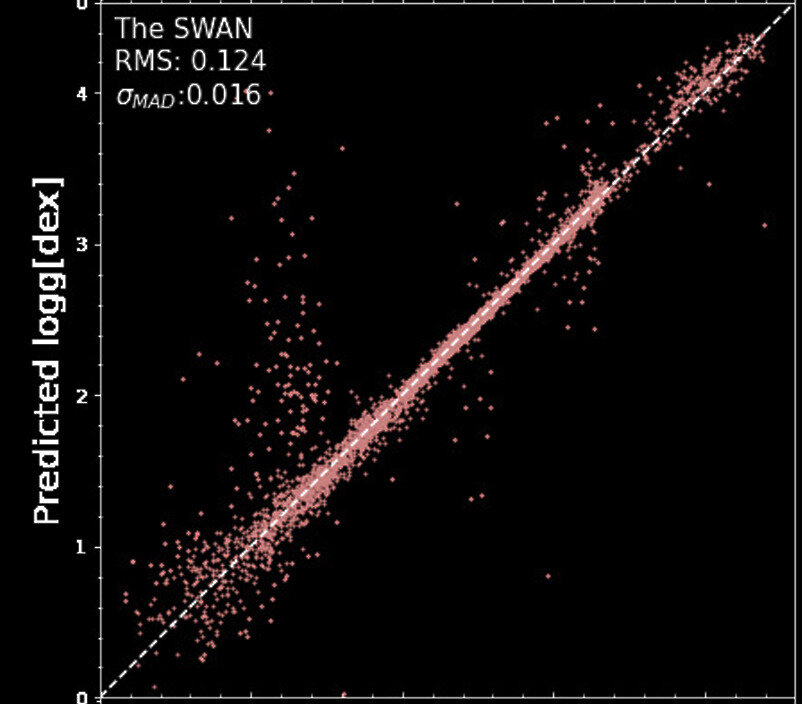
Transformer models surpass state-of-the-art algorithms

Kepler's Light Curve

0

1

2

3

4

0

1

2

3

4

Ground Truth Surface Gravity

0

1

2

3

4

Inferred Surface Gravity

State-of-the-art

This study

Pan, YST & Yu 22, 24a

Precise inductive bias drives the development of scalable models

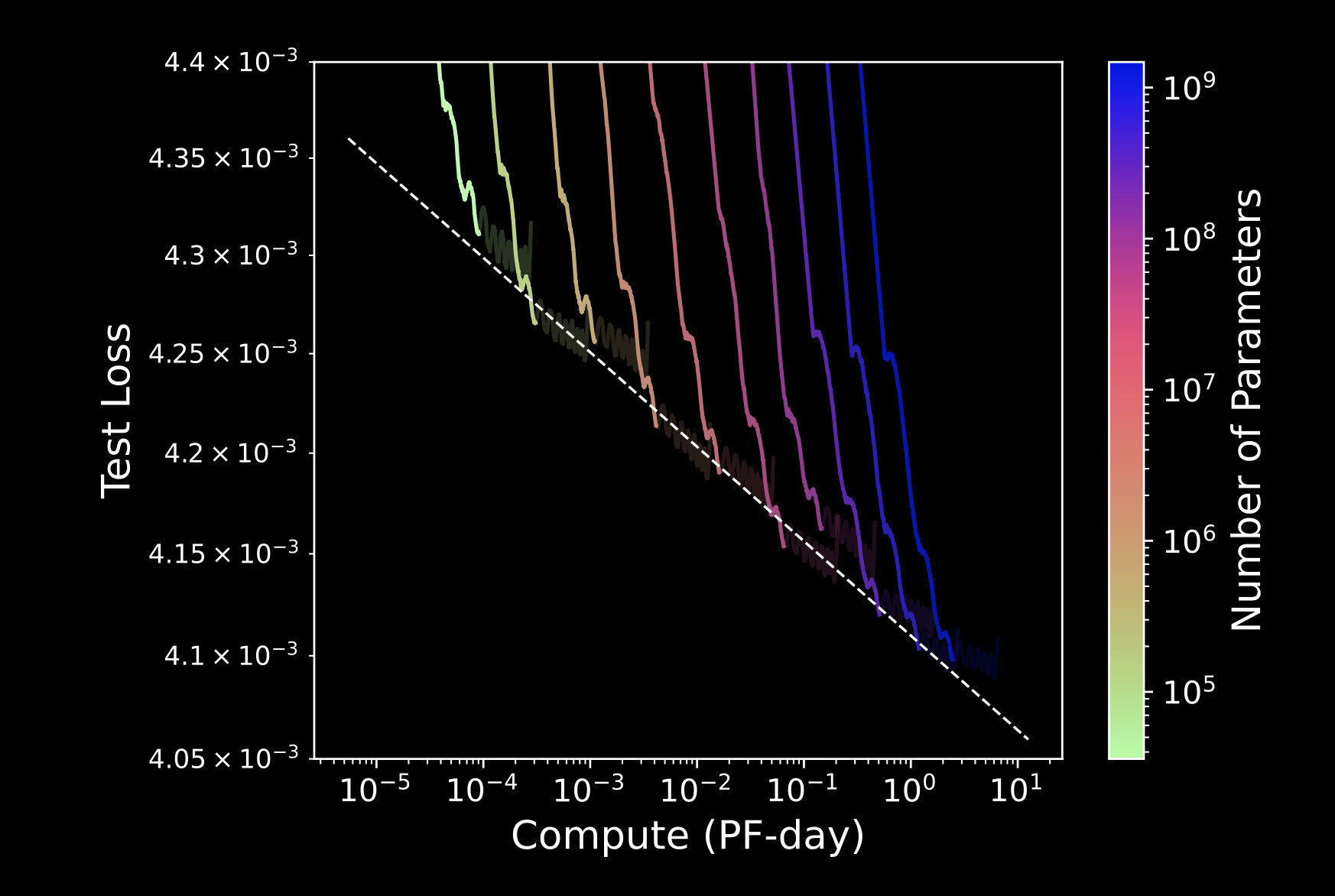
Neural Scaling Law also
applies to astronomical
time series data

Pan, YST & Yu, 24b

Open-AI, 2023

We can forecast and extrapolate the performance

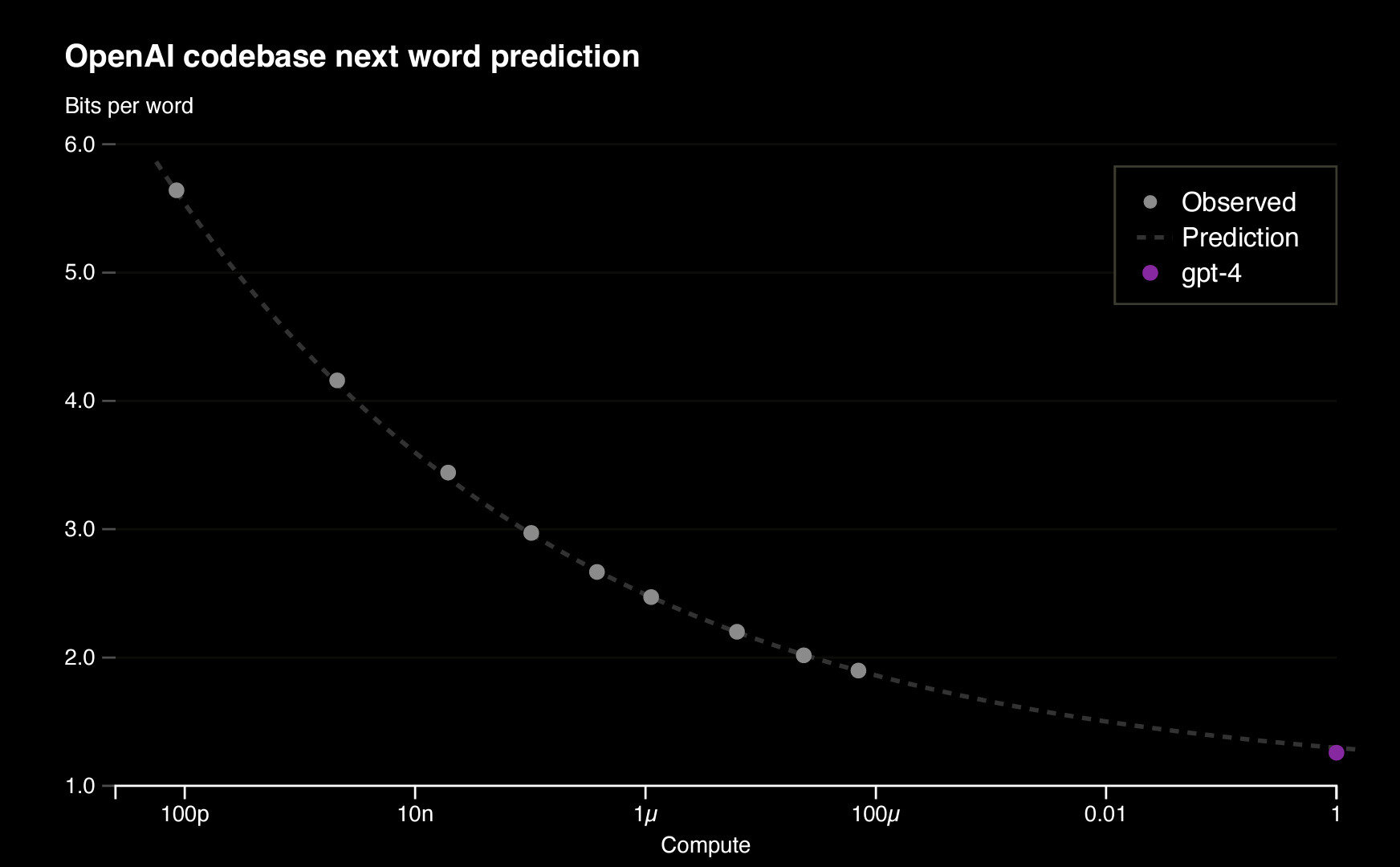
 "Model Size "

Performance

Know your inductive biases

Spectra also contain long-range information

Transformers result in improved generative models for spectra

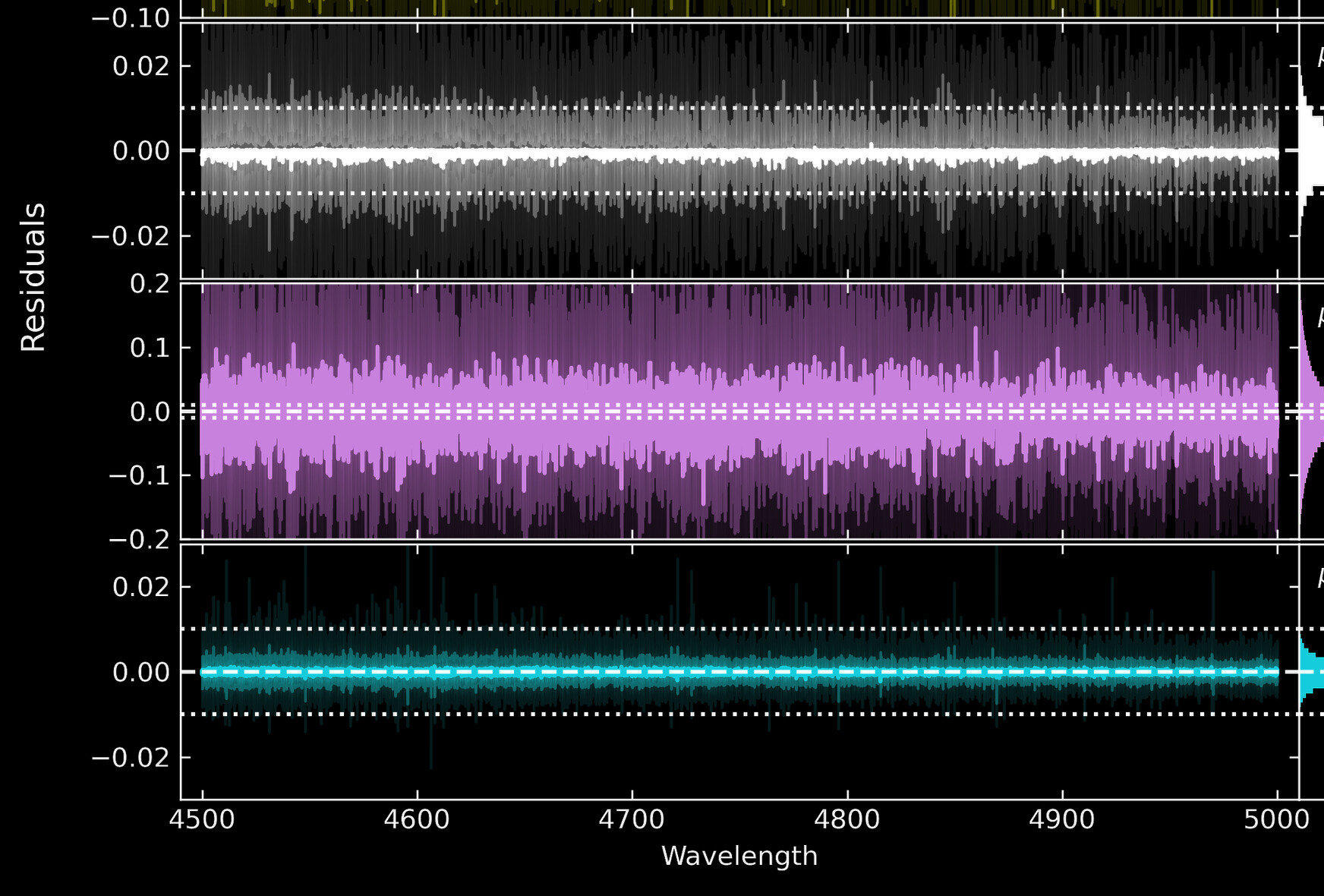
4500

4600

4700

4800

4900

5000

Wavelength [A]

Generative Residual [dex]

-0.02

0

0.02

0

-0.1

0.1

-0.02

0

0.02

Transformers

Convolutional Neural Networks

Multi-Layer Perceptron

Rozanski, YST+ 2024

Transformers also exhibit no signs of saturation during training

The more computing power we can allocate, the more the models will continue to improve

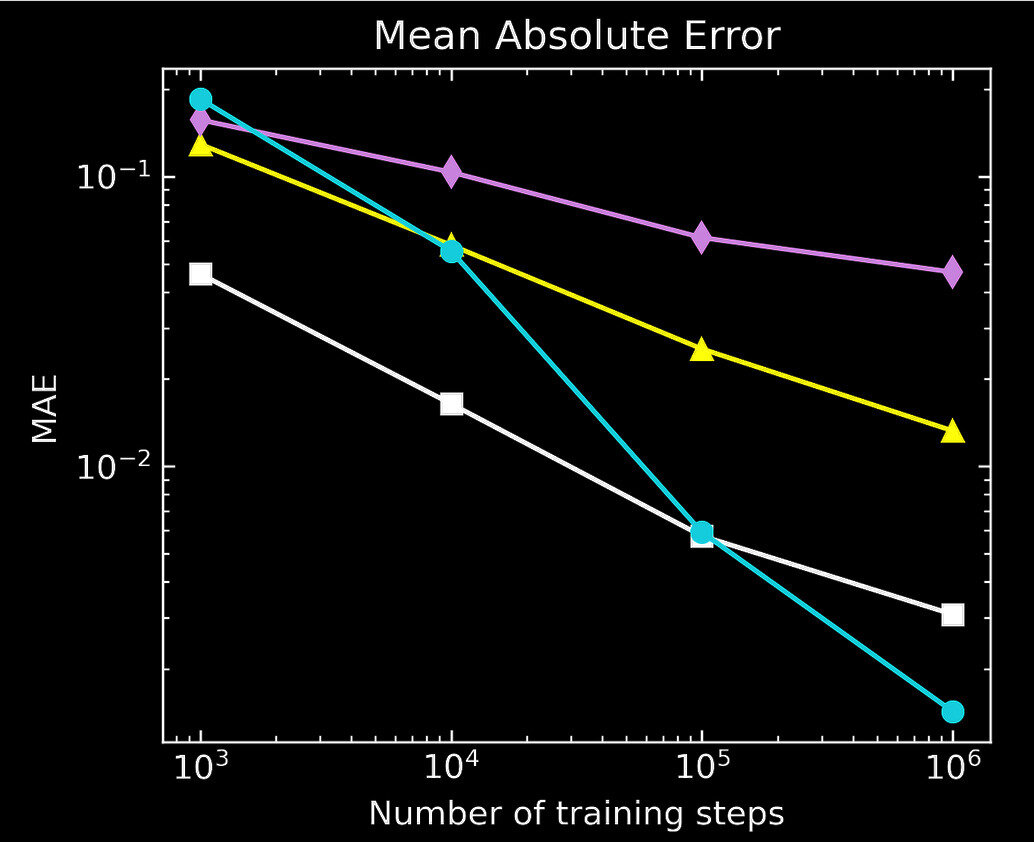
Number of Training Steps

10

3

10

4

10

5

10

6

Mean Absolute Error

10

-2

10

-1

Transformers

Multilayer-Perceptron

Transformers

CNN

Rozanski, YST+ 2024

Extracting Information from Low-Resolution DESI Spectra

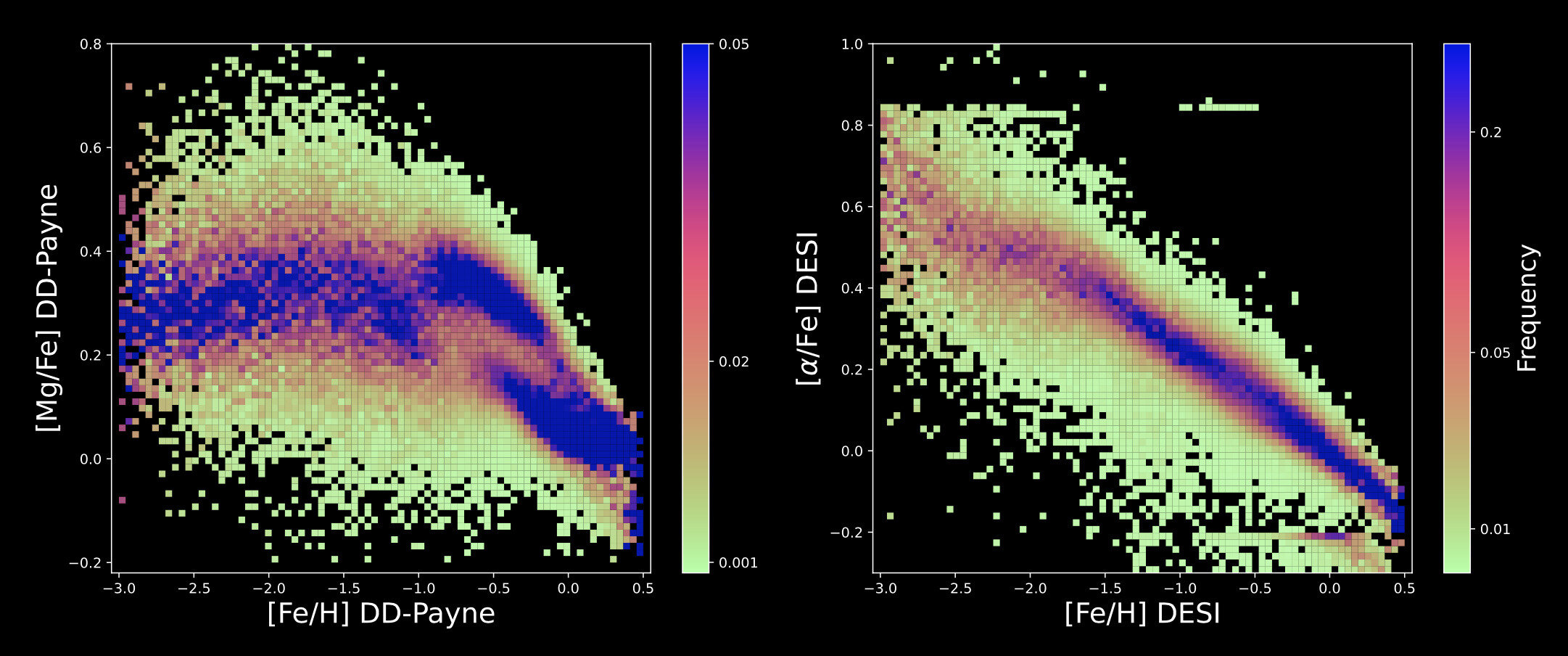
This Study

Classical Pipeline

Zhang, Xiang, YST+ 24

[Fe/H]

-3

-2

-1

0

-3

-2

-1

0

-3

-2

-1

0

-0.2

0.0

0.2

0.4

0.6

0.8

[Mg/Fe]

[Mg/Fe]

Thick Disk

Thin Disk

Gaia-Sausage-Enceladus

Fail to extract detailed structures

-0.2

0.0

0.2

0.4

0.6

0.8

[Mg/Fe]

Physics-Inspired Neural Networks

The fundamentals of Galactic dynamics

\frac{{\rm d} f}{{\rm d} t}

Distribution Function of 6D phase space

= \frac{\partial f}{\partial t} + v^i \frac{\partial f}{\partial x_i} - \frac{\partial \Phi}{\partial x^i} \frac{\partial f}{\partial v_i}

Gravitational Potential

= 0

(1) Liouville's Theorem

= 0

(2) Stationary

i.e., the system is collisionless

Deep-Potential: Encoding physics into neural networks

\frac{{\rm d} f}{{\rm d} t}
= \frac{\partial f}{\partial t} + v^i \frac{\partial f}{\partial x_i} - \frac{\partial \Phi}{\partial x^i} \frac{\partial f}{\partial v_i}

"Penalty" function: minimize

Green & YST+ 20 NeurIPS, 23

Inferring potential from  the distribution function of phase-space tracers

\sim 0

= 0

(1) Liouville's Theorem

= 0

(2) Stationary

i.e., the system is collisionless

\Phi

Gravitational potential

r

(represented by a neural network)

\Big\{ \frac{\partial f}{\partial x_i}, \frac{\partial f}{\partial v_i} \Big\}

0.0

-0.5

-1.0

0.1

10

x

y

-4

4

-4

4

\Big\{ \frac{\partial \Phi}{\partial x_i} \Big\}

True solution

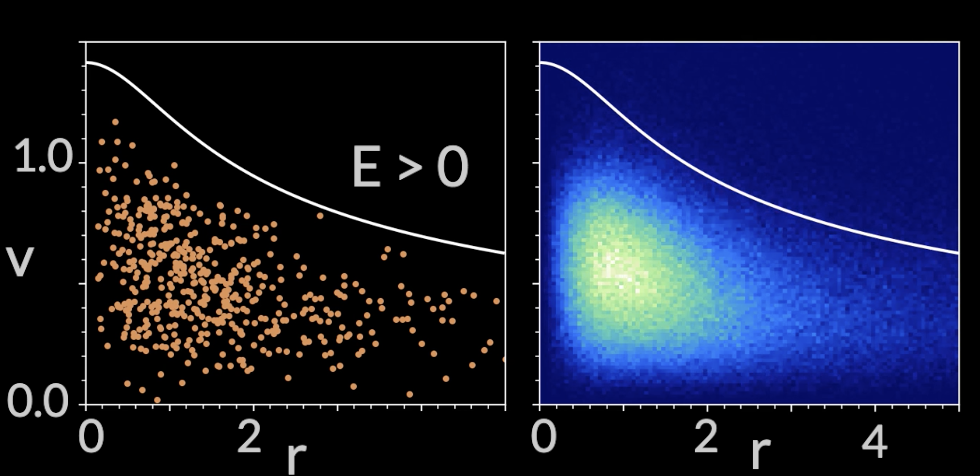
| v^i \frac{\partial f}{\partial x_i} - \frac{\partial \Phi}{\partial x^i} \frac{\partial f}{\partial v_i} |
\argmin_\Phi

Going beyond ansatz for distribution functions and potential

1.0

1.5

0.5

0.0

v

0

2

4

r

0

2

4

r

Green & YST+ 20 NeurIPS W, 23

4

Input : Phase-space tracers

\{ x_i, v_i \}_j

Output: Gravitational potential

\Phi(x)

while satisfying the Liouville theorem and being stationary

Green & YST+ 20 NeurIPS W, 23

Going beyond ansatz for distribution functions and potential

Mapping non-axisymmetric density of the Milky Way's halo

N-body Simulations

Deep Potential Recovery

x [kpc]

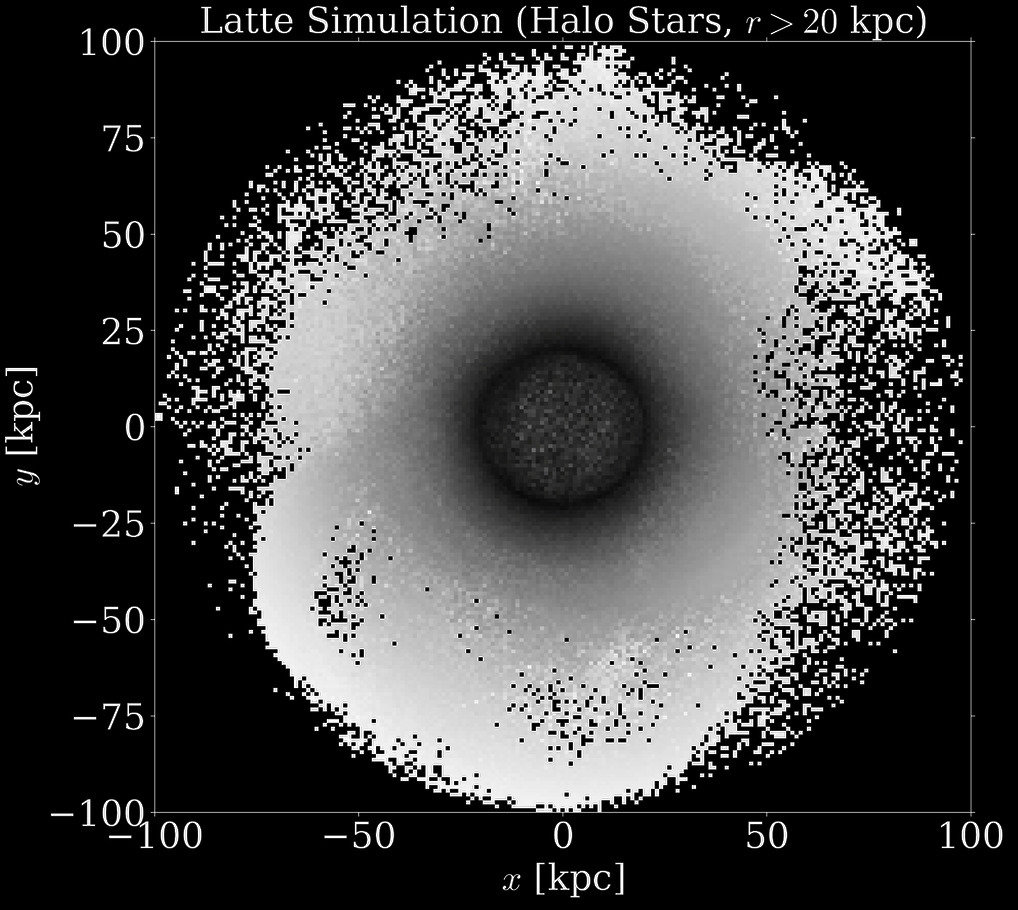
y [kpc]

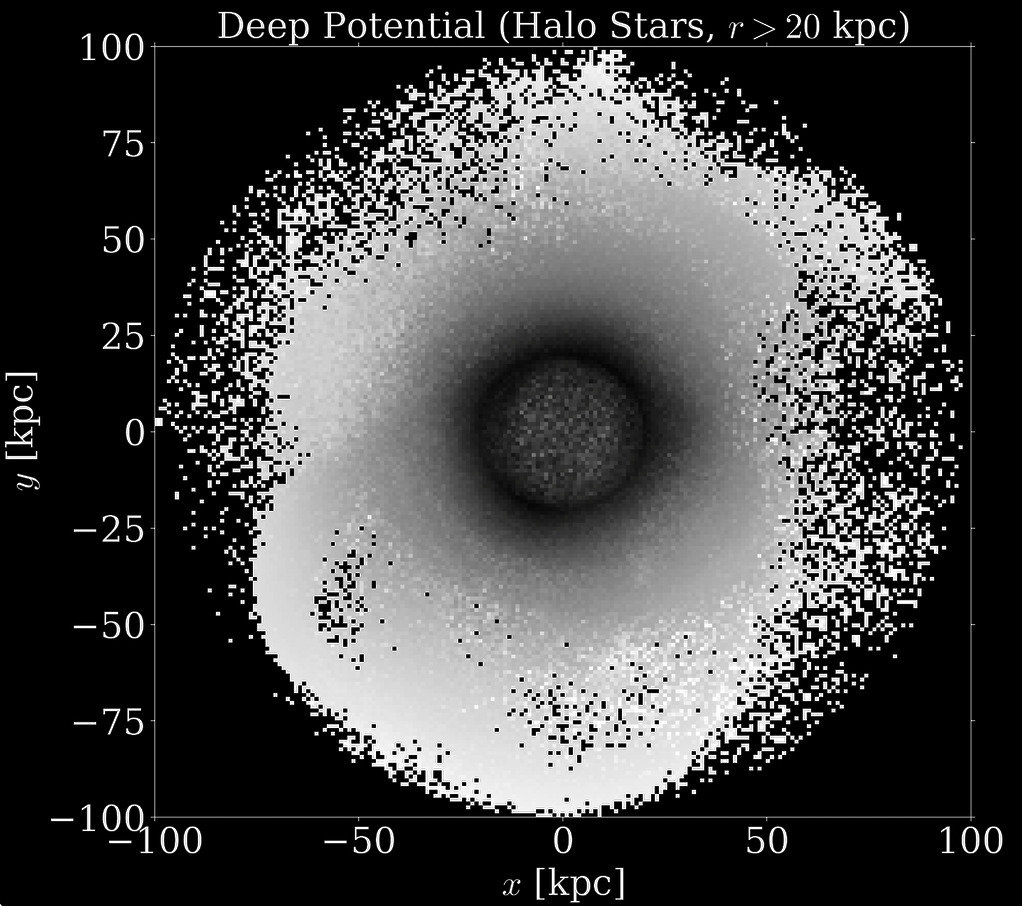
x [kpc]

Observation

Physics

Summary Statistics

Theory

Simulation

= Information Loss

Overcoming the curse of dimensionality
- (1 ) Symmetries
- (2) Physics-Inspired NN

p( {\rm obs} \, | \, {\rm physics} )

Generative Models

OpenAI's Sora

More statistically robust and "principled" deep learning approaches

e.g., YST & Weinberg 21, Ciuca & YST 22,
Tang & YST 22

Normalizing Flows
Diffusion Models

Modern deep learning are rooted in statistical principles

Are we willing to make the best inferences at the expense of "interpretability"?

"interpretable knowledge"

Accurate detection of cancer

"interpretable knowledge"

Finding a nearby alien race before they kill us off

"interpretable knowledge"

Predicting galaxy evolution

"interpretable knowledge"

Finding new physics ?

Simulations

Big Data

Deep Learning

Big Data

Simulations

Ted Chiang, Nature, 2000

How to best harness information from simulations ?

Credit : Illustris / TNG

Solution : GNN that respects group action symmetry

A technical slide that probably no one cares .....

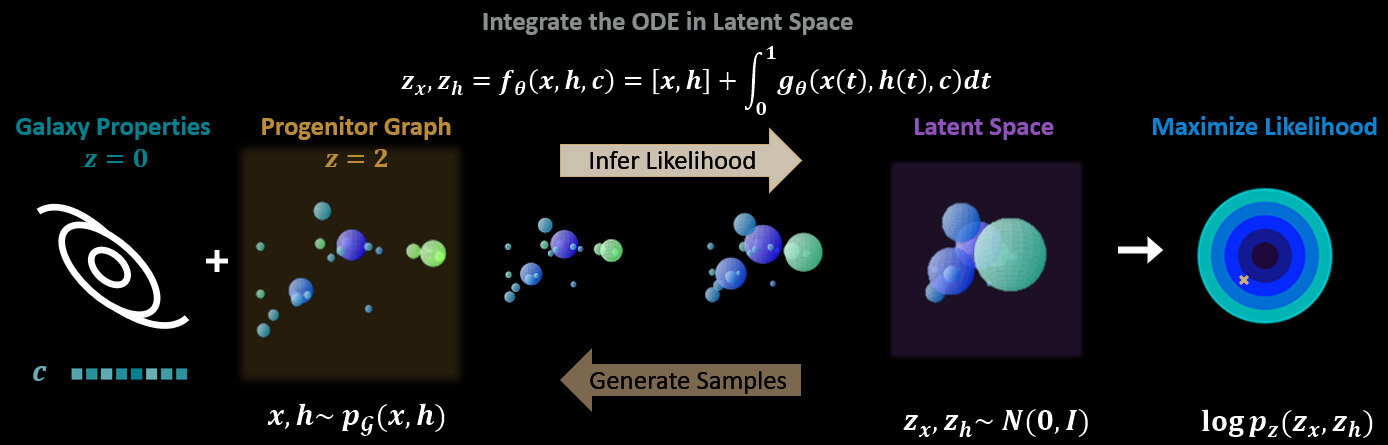
Neural ODE as Normalizing Flow

A technical slide that probably no one cares .....

Graph Neural Network as the integrand

- Can vary in dimension

A technical slide that probably no one cares .....

The message passing function satisfies E(n) equivariances

Graph Neural Networks

Normalizing Flow

Physics INN

Equivariances

SBI

Have we learned the marginal distribution accurately ?

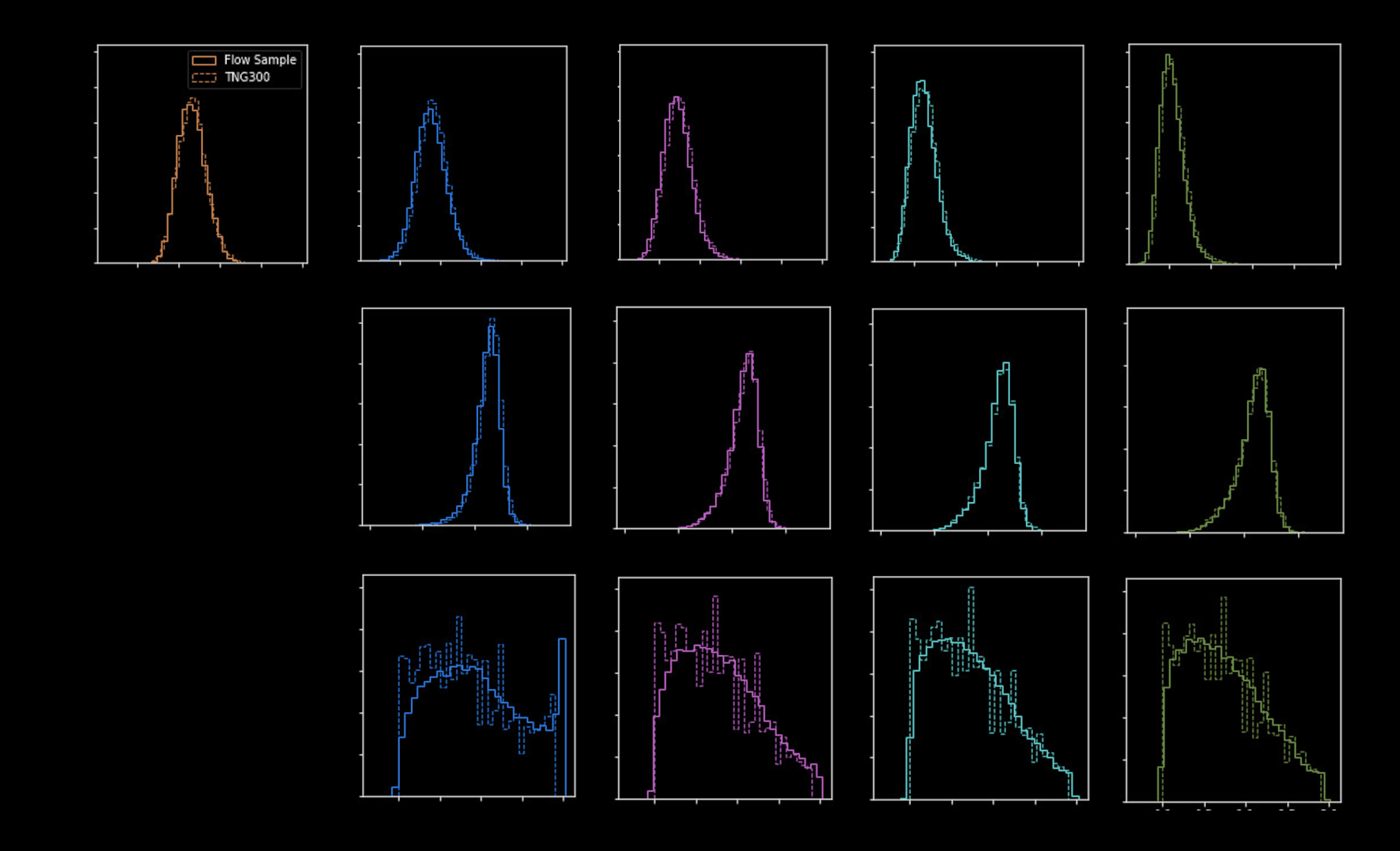
Main Progenitor

1st Merger

2nd Merger

3rd Merger

4th Merger

Stellar mass

Distance from the main progenitor

Merging redshift

Graph generated

TNG 300 simulations

Not possible by looking only at the most similar galaxies in the simulation

Correlations
smeared out

Distilling knowledge from simulations

Distilling knowledge from simulations

The Milky Way

All the progenitors that can make the Milky Way

M0

M1

M4

M2

M3

z1

z2

z3

z4

M0

Progenitor Mass

Merging
Redshift

Pairwise Separation

Progenitor
Mass

Merging
Redshift

M1

d02

M2

M3

M4

z1

z2

z3

z4

Limited by the
sampling noise

d01

d03

d04

d12

d13

d14

d23

d24

d34

Correlation

-0.5

-0.1

0

0.1

0.5

200 "closest" samples from TNG300

5000 "closest" samples from TNG300

M0

M1

M4

M2

M3

z1

z2

z3

z4

M0

Progenitor Mass

Merging
Redshift

Progenitor
Mass

Merging
Redshift

M1

d02

M2

M3

M4

z1

z2

z3

z4

Too distinct from
the reference point

d01

d03

d04

d12

d13

d14

d23

d24

d34

Correlation

-0.5

-0.1

0

0.1

0.5

Pairwise Separation

From graph generative models

M0

M1

M4

M2

M3

z1

z2

z3

z4

M0

Progenitor Mass

Merging
Redshift

Progenitor
Mass

Merging
Redshift

M1

d02

M2

M3

M4

z1

z2

z3

z4

d01

d03

d04

d12

d13

d14

d23

d24

d34

Correlation

-0.5

-0.1

0

0.1

0.5

A massive main progenitor requires a latter merger to compensate 

Pairwise Separation

If the first massive merger happens earlier, the other mergers have to be more massive to compensate

How to identify one-in-a-billion outliers?

Finding interesting outliers which physics are not known

Finding interesting outliers which physics are not known

Phew.... we still needs human to intepret

Source: AI Index Report 2024

2013

2015

2017

2017

2019

2021

2023

0%

20%

40%

60%

80%

100%

Year

human baseline

Image classification

Basic-level reading comprehension

Multitask language understanding

Mathematical reasoning

Performance vs. human

Observed data

Synthetic models

Overcoming model imperfections using domain adaptation

"Observed data"

"Synthetic models"

Overcoming model imperfections using domain adaptation

Overcoming model imperfections using domain adaptation

Overcoming model imperfections using domain adaptation

Closing the synthetic-observation gap with domain adaptation

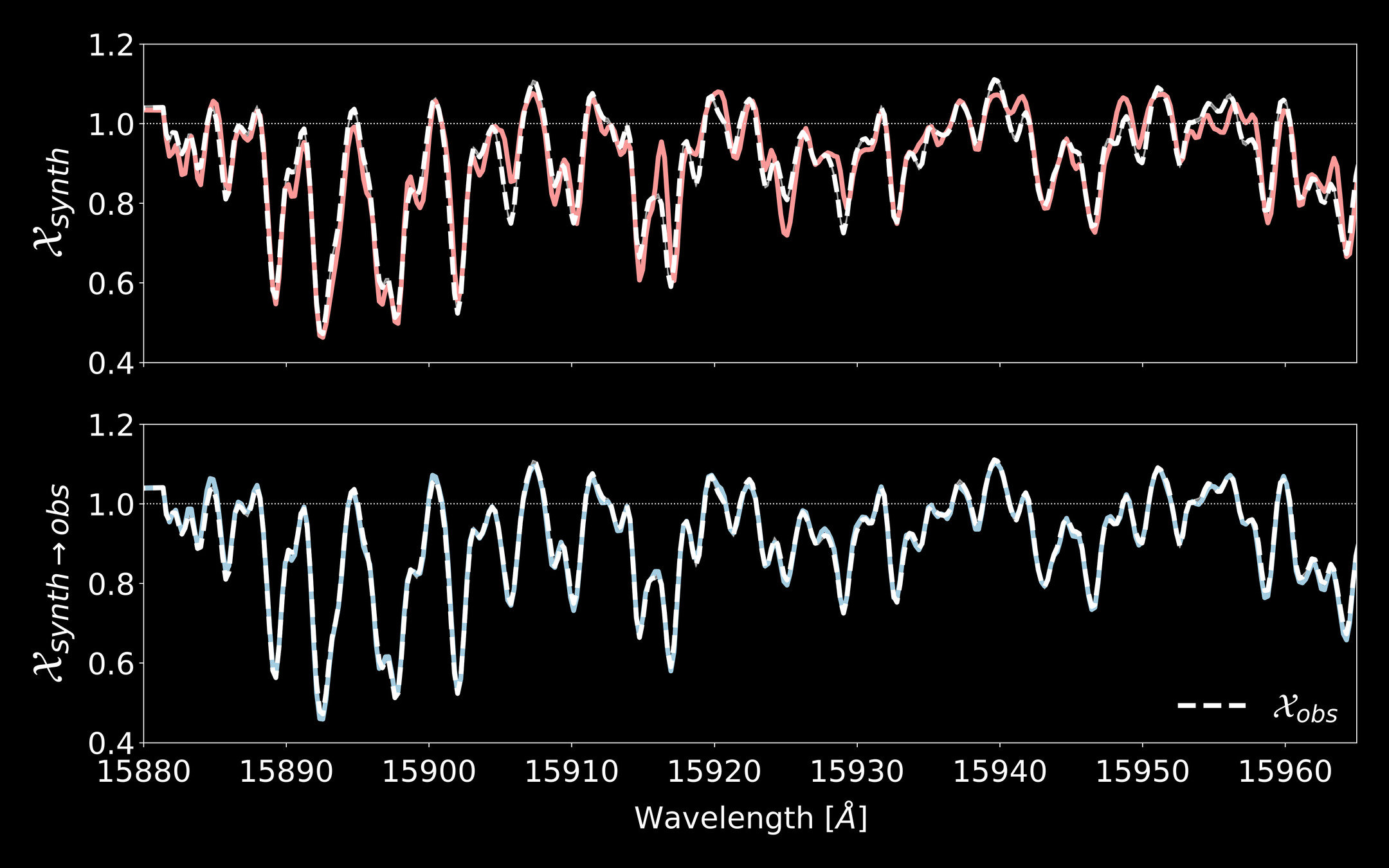
0.5

1.0

0.5

1.0

15900

15950

APOGEE

Kurucz model

Normalized Spectrum

Domain adaptation

Wavelength [A]

 , YST+ 2020, ICML

O'Briain

APOGEE

M-dwarfs are hard!